# A tibble: 103 x 8
id acceptyear age survived survtime prior transplant wait
<int> <int> <int> <fct> <int> <fct> <fct> <int>
1 15 68 53 dead 1 no control NA
2 43 70 43 dead 2 no control NA
3 61 71 52 dead 2 no control NA
4 75 72 52 dead 2 no control NA
5 6 68 54 dead 3 no control NA
6 42 70 36 dead 3 no control NA
7 54 71 47 dead 3 no control NA
8 38 70 41 dead 5 no treatment 5
9 85 73 47 dead 5 no control NA
10 2 68 51 dead 6 no control NA
# ... with 93 more rowsLogistic Regression
STA 101L - Summer I 2022
Raphael Morsomme
Welcome
Announcements
Recap
Simple and multiple lrm
- numerical response
model selection
overall criterion
predictive performance
stepwise procedures
Outline
- Modeling a binary response
- Logistic regression
- One predictor
- Multiple predictors
Modeling a binary response
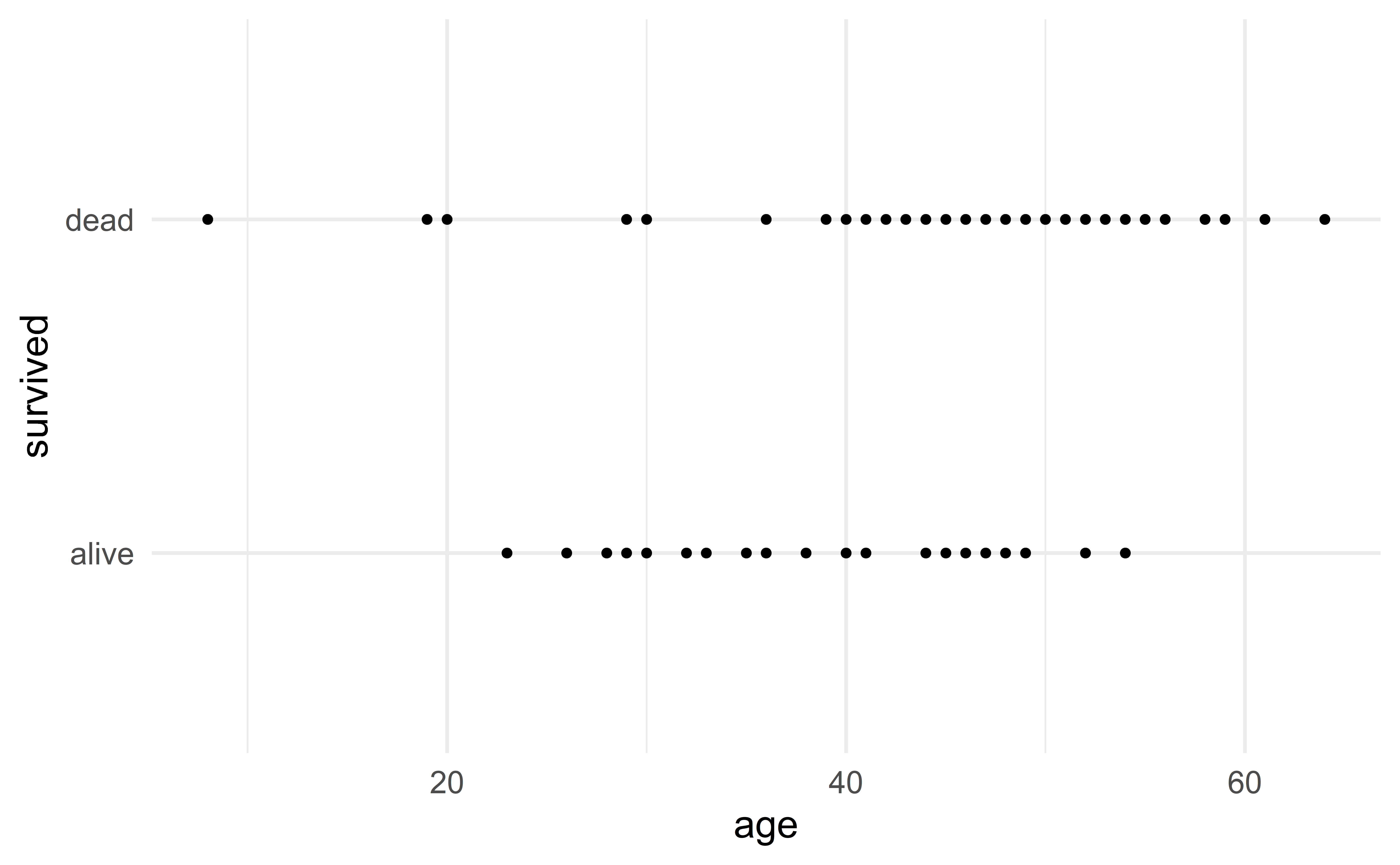
Example – Stanford University Heart Transplant Study
Goals: to determine whether an experimental heart transplant program increases lifespan
observations: patients
response: survival after 5 years (binary)
predictors: age, prior surgery, waiting time for transplant.
Data
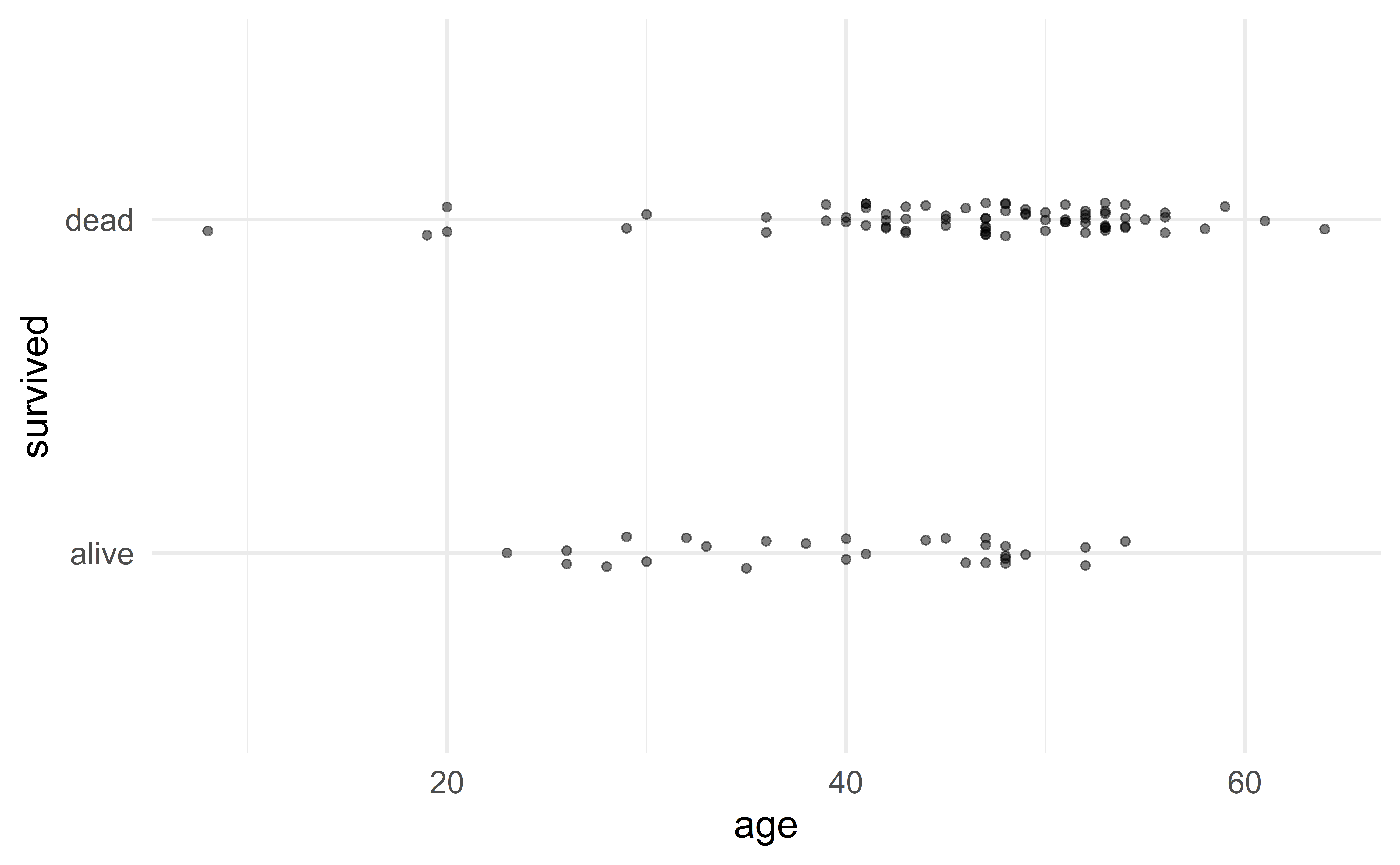
Effect of age on survival
Binary response
Technical problem: levels of the response are labels
- can’t fit a regression model to words, only to numbers
use
mutateto create a binary variable (either 0 or 1)
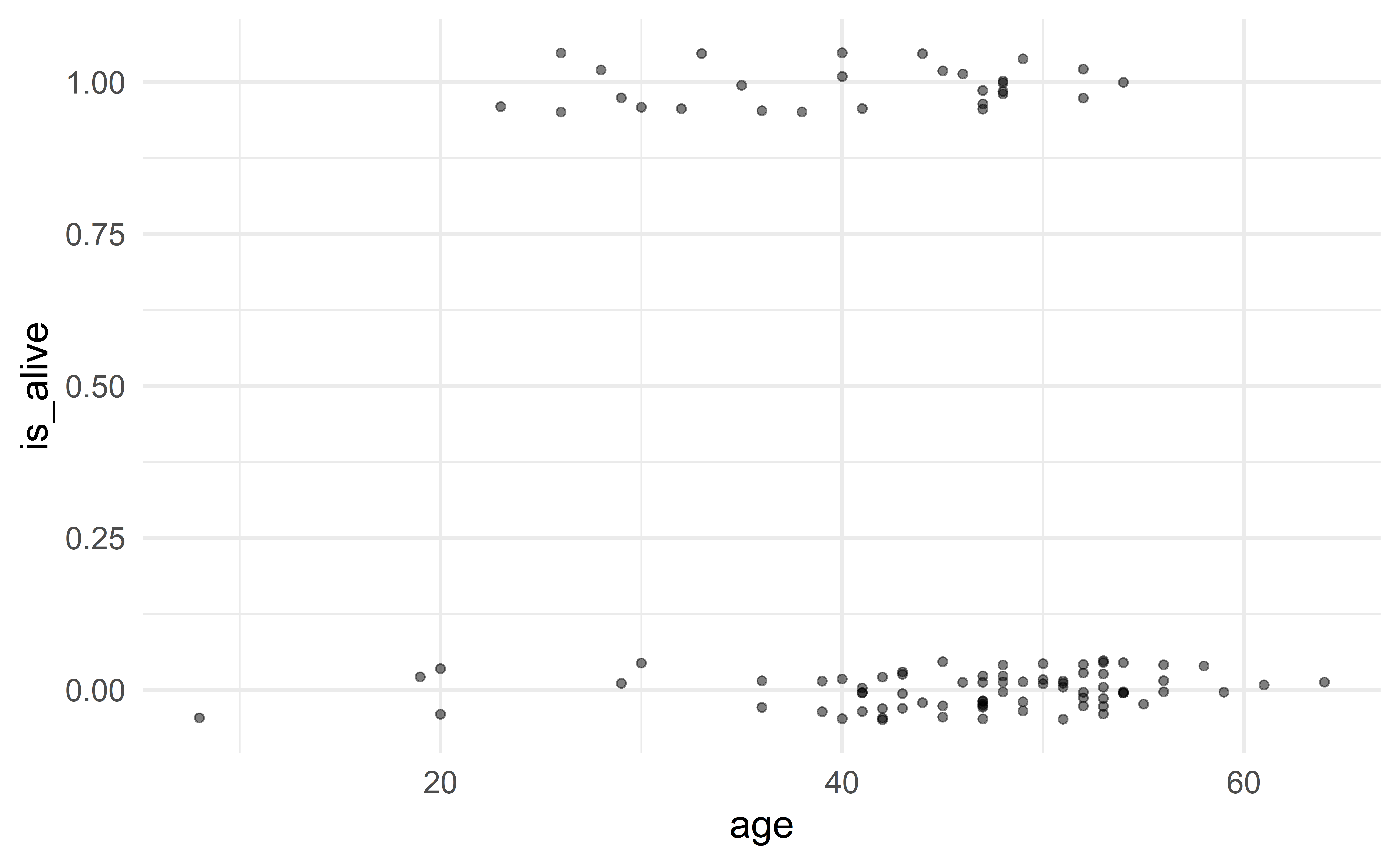
Linear regression?
Intuitively, age should be a good predictor of survival.
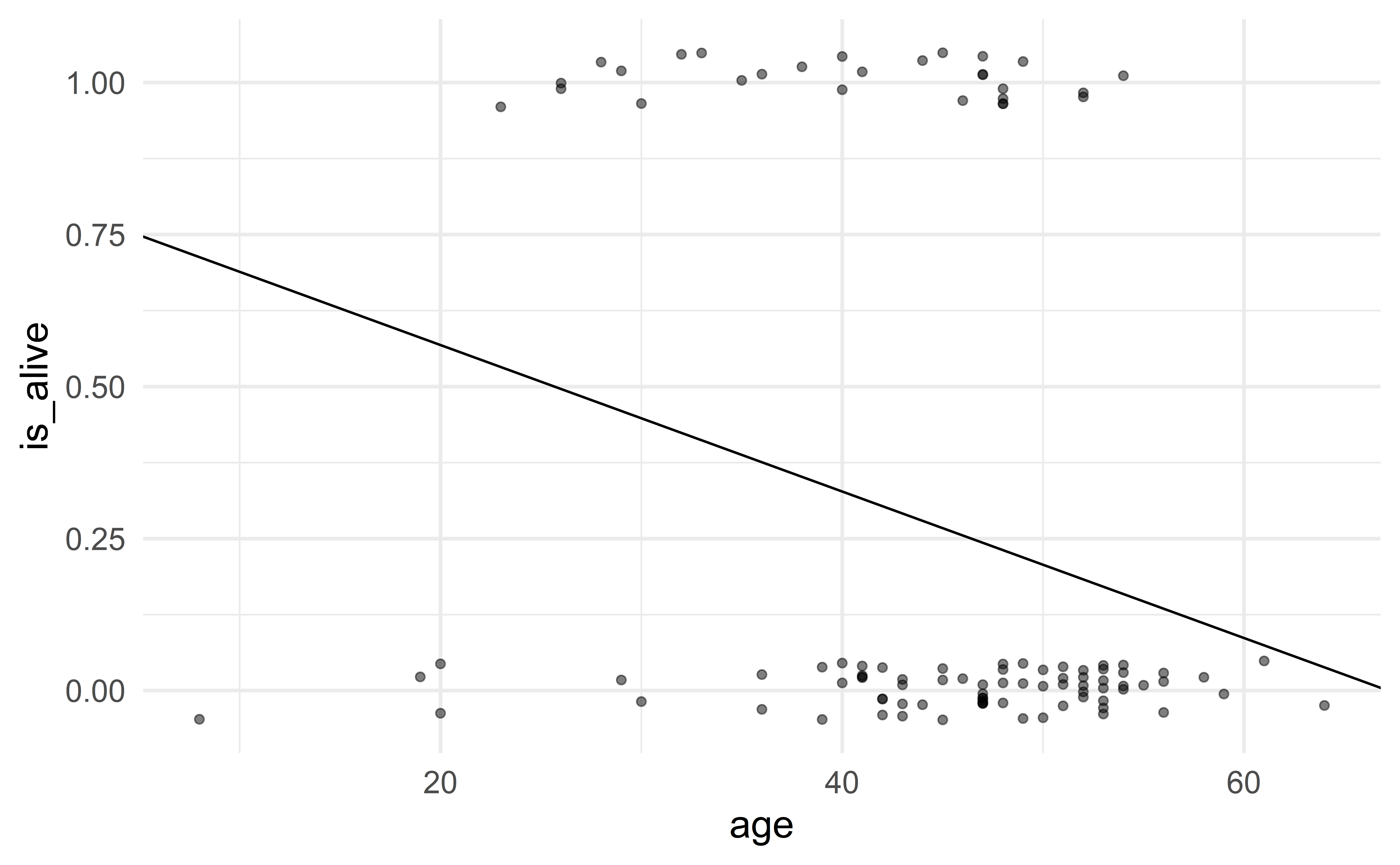
Problems with linear regression
The response is not continuous
- unlike fuel consumption, tree volume or newborn weight
nonsensical predictions, even for reasonable value of
age.
Group exercise - limitation of linear regression
What is the prediction for a 70-year-old patient?
02:00
Generalized linear models
GLMs
Generalized linear models (GLMs – STA310) extend the linear regression framework to settings where the response variable is restricted:
logistic regression with binary response
multinomial regression with nominal (categorical) response, e.g. voting in multiparty systems
ordinal regression with ordinal (categorical) response, e.g. course letter grade
poisson regression with count response, e.g. number of children
gamma regression with positive response variable, e.g. mpg, insurance costs
beta regression with continuous response between 0 and 1 (percentage), e.g. cancer rates in counties
Logistic regression
Logistic regression
Example of a generalized linear model
We’ll focus on implementation and interpretation
Useful for inference project (not the prediction project)
Logistic regression: model the probability of success \(p\) based on a set of predictors \(X_1, \dots, X_p\).
Binary outcome and probability
Let \(Y_i\) denote the response of person \(i\).
The logistic regression model assumes that
\[ Y_i = \begin{cases} 1 \text{ (success)}, \text{with probability } p_i, \\ 0 \text{ (failure)}, \text{with probability } 1-p_i. \end{cases} \]
where \(p_i\) denotes the probability of success (survival) of person \(i\).
Modeling a probability with linear regression?
We saw that we cannot model \(p\) with a lrm (\(p \approx \beta_0 + \beta_1\text{age}\))
\(0\le p_i\le1\)
…but \(\beta_0 + \beta_1 \text{age}\) may be negative or larger than 1!
- in fact, the regression line extends infinitely in either either direction
Warning
Binary variables should not be modeled using linear regression!
Modeling a probability with logistic regression
Intuitively, an older patient should have a smaller probability of surviving.
\(\Rightarrow\) We want a model that associates a smaller probability \(p\) for a patient with a larger year variable.
\(\Rightarrow\) We need to find a way to go from age (could be any number) to \(p\) (between 0 and 1)
The logit transformation
Consider the logit transformation
\[ p = \dfrac{e^{\mu}}{1+e^{\mu}} \]
where \(\mu\) can be any number.
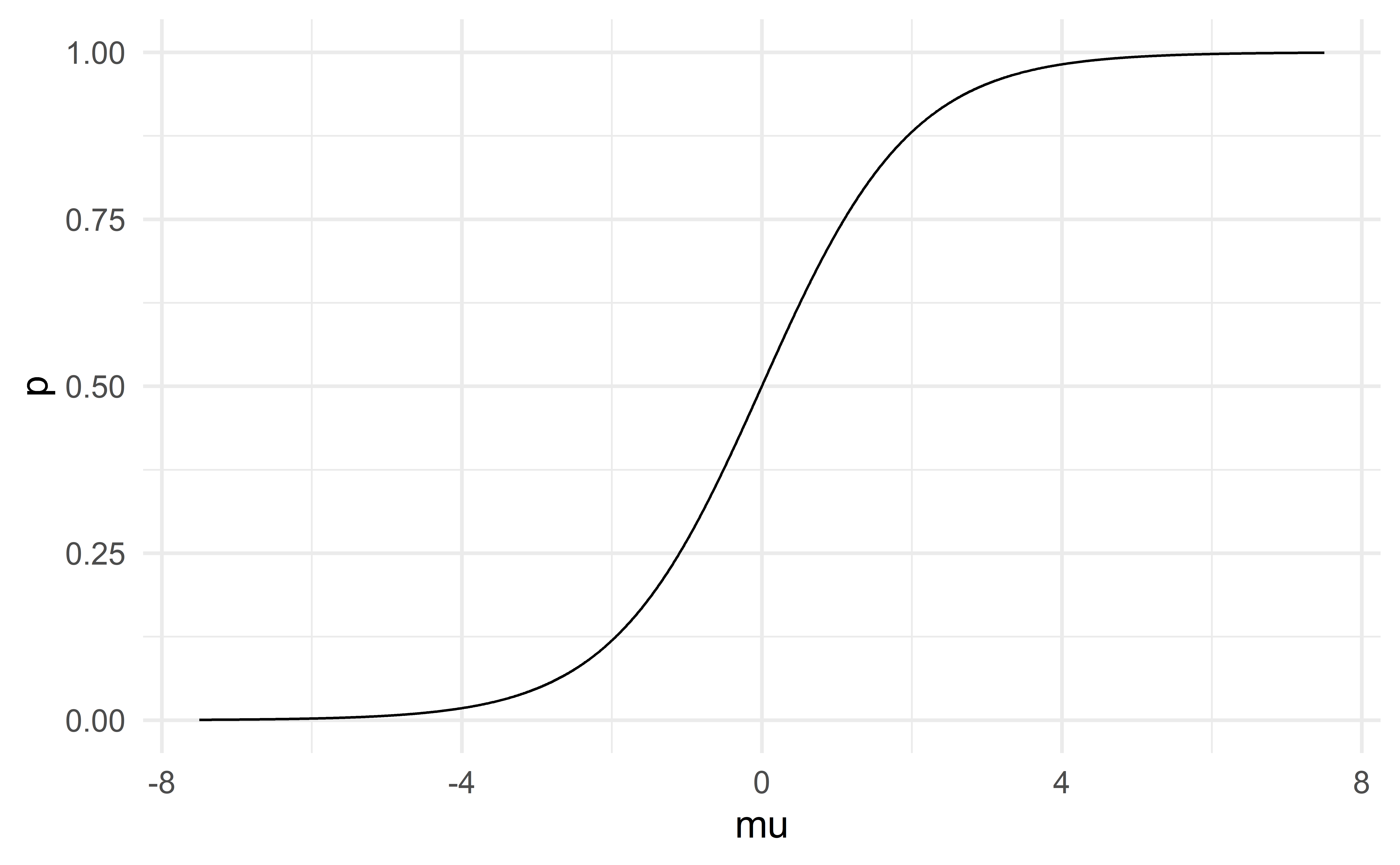
Note that \(\dfrac{e^{\mu}}{1+e^{\mu}}\) is bounded between 0 and 1.
Moreover, larger values of \(\mu\) will give larger \(p\), and smaller \(\mu\) will give smaller \(p\).
Group exercise - logit transformation
What value of \(p\) corresponds to
\(\mu = 0.5\)?
\(\mu = 2\)?
\(\mu = -2\)?
What value of \(\mu\) gives
\(p=0.5\)?
\(p=0.9\)?
\(p=0.1\)?
03:00
Modeling \(\mu\)
We can now simply model \(\mu\) using a simple lrm with age
\[ \mu \approx \beta_0 + \beta_1 \text{age} \]
and then transform \(\mu\) into \(p\) using the logit transformation
\[ p = \dfrac{e^{\mu}}{1+e^{\mu}} \]
Putting everything together gives the logistic regression model
\[ p = \dfrac{e^{\mu}}{1+e^{\mu}} \approx \dfrac{e^{\beta_0 + \beta_1 \text{age}}}{1+e^{\beta_0 + \beta_1 \text{age}}} \]
Alternative formulation
The formulation
\[ \log\left(\frac{p}{1-p}\right) \approx \beta_0 +\beta_1 \text{age} \]
is also widely to describe the logistic regression model. This formulation is equivalent to that used on the previous slide.
Maximum likelihood estimates
How are the unknown coefficients \(\beta_0\) and \(\beta_1\) estimated?
When we fit a logistic regression model with R, the so-called maximum likelihood estimates (MLE1) are returned.
Implementation
glm
We fit a logistic regression model in R with the command glm (not lm)
Call: glm(formula = is_alive ~ age, family = binomial, data = d)
Coefficients:
(Intercept) age
1.56438 -0.05847
Degrees of Freedom: 102 Total (i.e. Null); 101 Residual
Null Deviance: 120.5
Residual Deviance: 113.7 AIC: 117.7R output
For the moment simply focus on
coefficient estimates
AIC (no (adjusted-) \(R^2\)) for model selection
glm not lm
To fit a logistic regression model in R, use the command glm (not lm) with the argument family = binomial.
Interpretation
A positive coefficient estimate indicates that a higher value of the predictor is associated with a higher probability of success; and vice-versa for a smaller value.
In our case, the coefficient estimate for age (-0.058) is negative, so the model indicates that older participants have a smaller probability of surviving.
Visualizing the regression curve
# A tibble: 103 x 8
is_alive age .fitted .resid .std.resid .hat .sigma .cooksd
<dbl> <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0 53 0.177 -0.625 -0.630 0.0156 1.06 0.00174
2 0 43 0.279 -0.809 -0.813 0.0106 1.06 0.00210
3 0 52 0.186 -0.642 -0.646 0.0147 1.06 0.00173
4 0 52 0.186 -0.642 -0.646 0.0147 1.06 0.00173
5 0 54 0.169 -0.608 -0.614 0.0166 1.06 0.00175
6 0 36 0.368 -0.958 -0.967 0.0181 1.06 0.00548
7 0 47 0.234 -0.731 -0.735 0.0111 1.06 0.00174
8 0 41 0.303 -0.850 -0.855 0.0115 1.06 0.00257
9 0 47 0.234 -0.731 -0.735 0.0111 1.06 0.00174
10 0 51 0.195 -0.659 -0.663 0.0138 1.06 0.00172
# ... with 93 more rows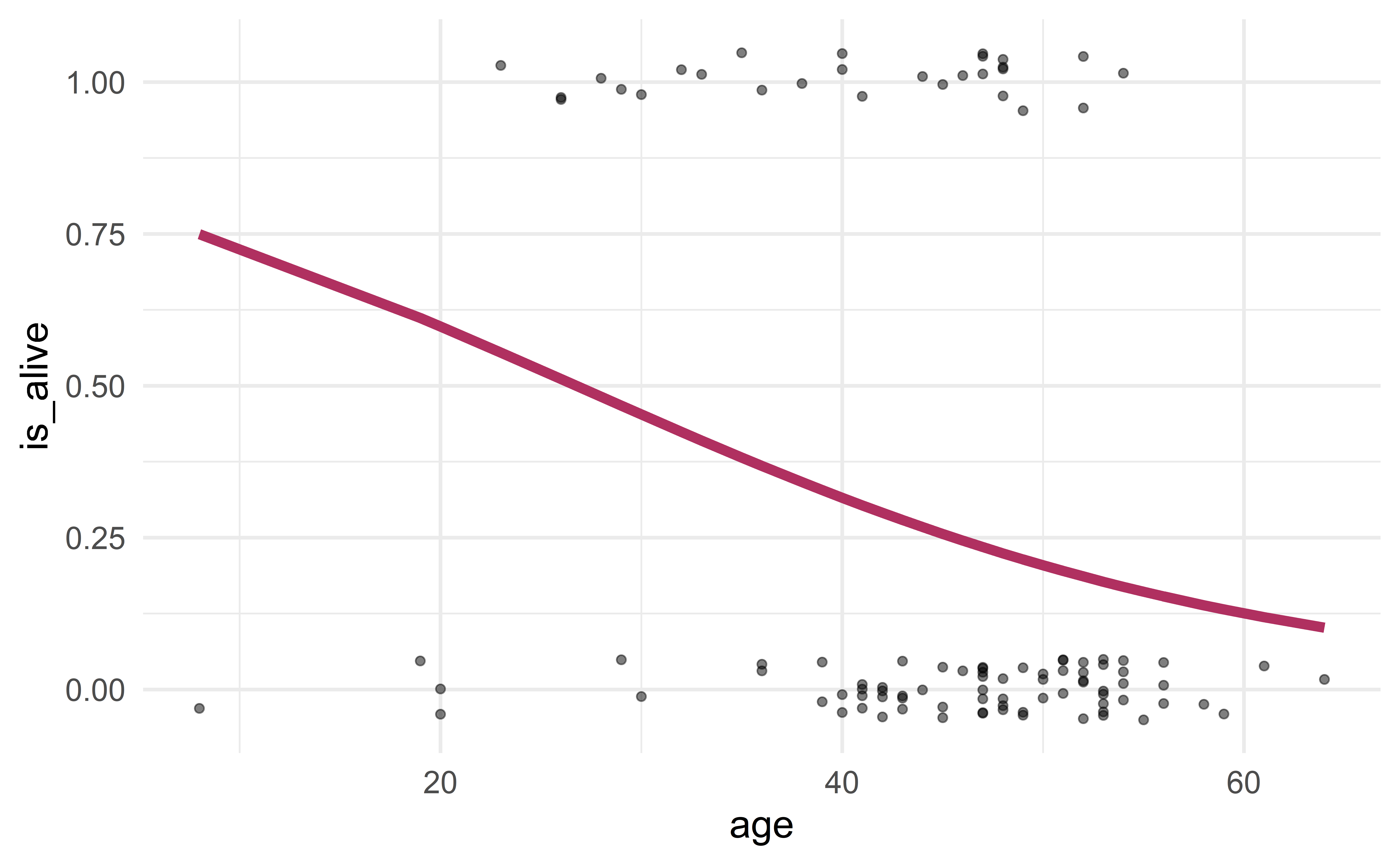
Extending the regression curve
#artificial data with larger range (0 to 100)
d_artificial <- tibble(age = seq(0, 100, by = 0.1))
p_hat <- predict(m, newdata = d_artificial, type = "response")
d_artificial <- mutate(d_artificial, p_hat = p_hat)
d_artificial# A tibble: 1,001 x 2
age p_hat
<dbl> <dbl>
1 0 0.827
2 0.1 0.826
3 0.2 0.825
4 0.3 0.824
5 0.4 0.824
6 0.5 0.823
7 0.6 0.822
8 0.7 0.821
9 0.8 0.820
10 0.9 0.819
# ... with 991 more rows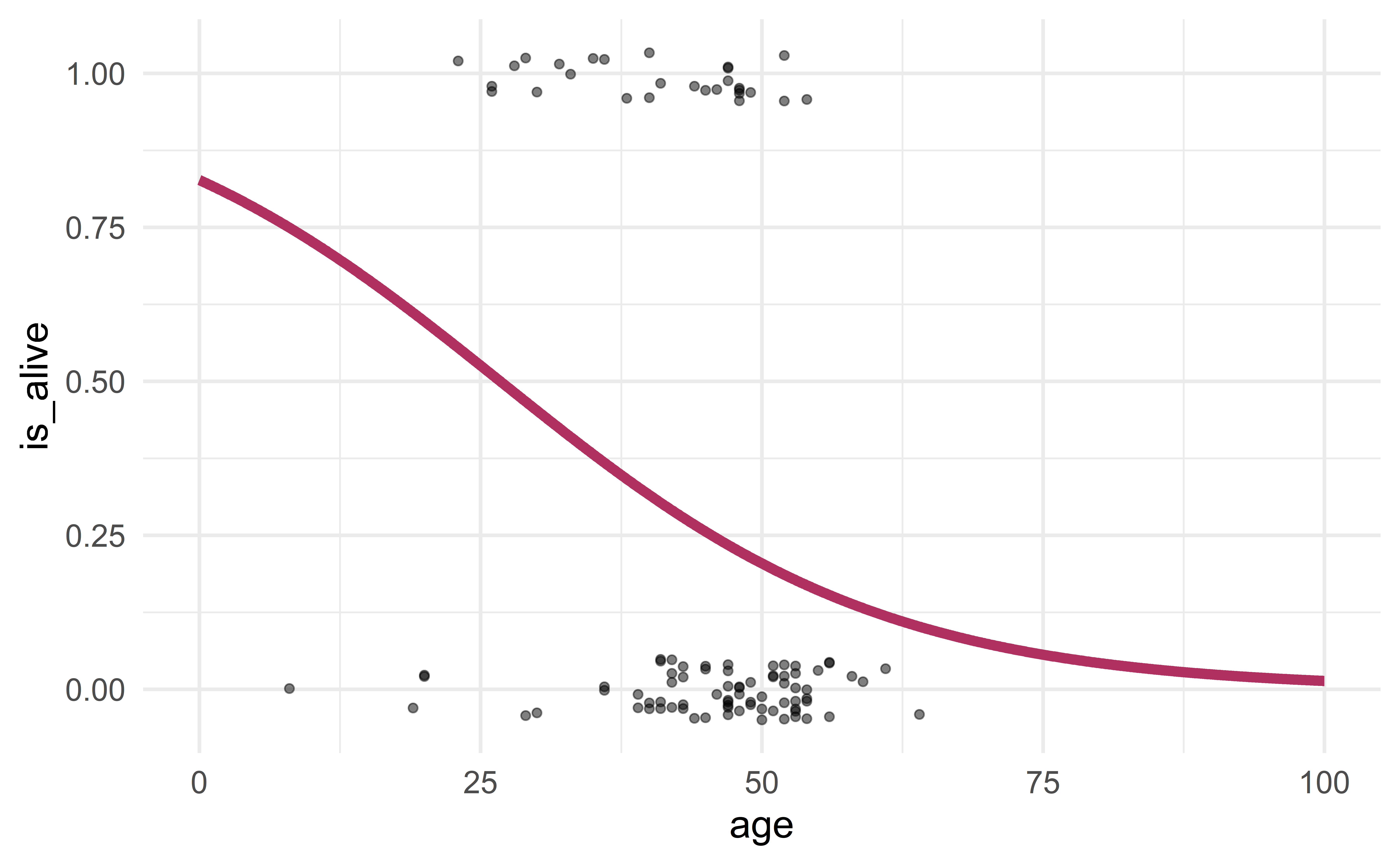
Multiple logistic regression
Based on what we know about multiple lrm, it is easy to extend the previous framework to multiple logistic regression:
\[ p = \dfrac{e^{\mu}}{1+e^{\mu}} \]
where
\[ \mu \approx \beta_0 + \beta_1 X_1 + \dots + \beta_p X_p \]
Implementation in R
m2 <- glm( # glm, not lm
is_alive ~ age + transplant,
family = binomial, # logistic regression
data = d
)
m2
Call: glm(formula = is_alive ~ age + transplant, family = binomial,
data = d)
Coefficients:
(Intercept) age transplanttreatment
0.97311 -0.07632 1.82316
Degrees of Freedom: 102 Total (i.e. Null); 100 Residual
Null Deviance: 120.5
Residual Deviance: 103.9 AIC: 109.9Group exercise - interpretation
What is the interpretation of the coefficient estimates for age and transplant?
02:00
Group exercise - interpretation
Exercise 9.5
04:00
Group exercise - implementation
Exercise 9.3
You do not need to do parts a and b.
Simply fit the two models in R. The possum data used in this exercise can be found in the openintro R package. You should obtain the same coefficient estimates as in the book, though with an opposite sign.
Save these models; you will need them later!
04:00
Artificial data
d_artificial <- expand.grid(
age = seq(0, 100, by = 0.1),
transplant = c("treatment", "control")
) %>%
as_tibble() %>%
arrange(age)
d_artificial# A tibble: 2,002 x 2
age transplant
<dbl> <fct>
1 0 treatment
2 0 control
3 0.1 treatment
4 0.1 control
5 0.2 treatment
6 0.2 control
7 0.3 treatment
8 0.3 control
9 0.4 treatment
10 0.4 control
# ... with 1,992 more rowsVisualization
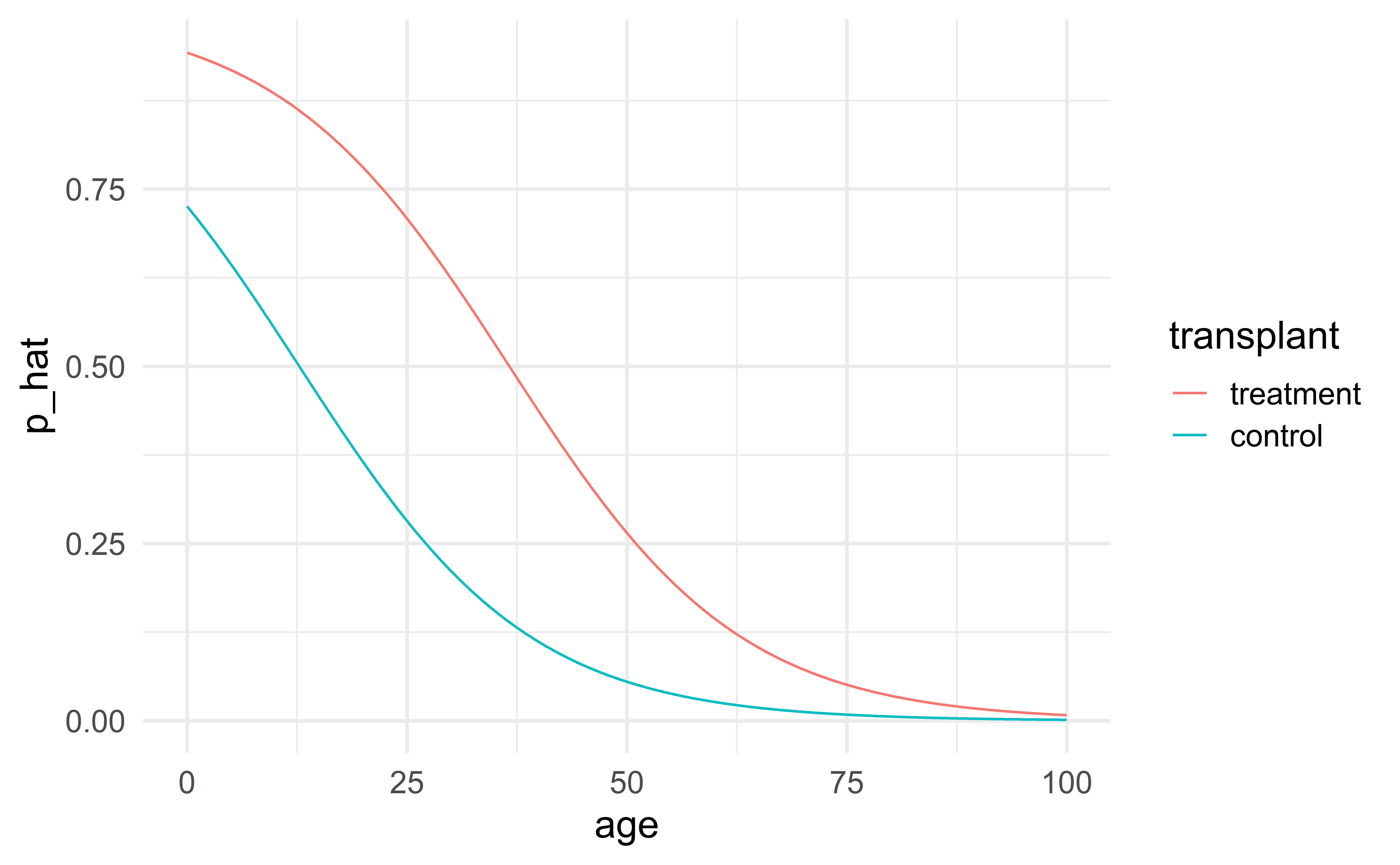
Prediction
d_augm <- augment(m2, type.predict = "response") %>%
mutate(is_alive_hat = if_else(.fitted < 0.5, 0, 1)) %>%
select(is_alive, age, transplant, .fitted, is_alive_hat)
d_augm# A tibble: 103 x 5
is_alive age transplant .fitted is_alive_hat
<dbl> <int> <fct> <dbl> <dbl>
1 0 53 control 0.0443 0
2 0 43 control 0.0904 0
3 0 52 control 0.0476 0
4 0 52 control 0.0476 0
5 0 54 control 0.0412 0
6 0 36 control 0.145 0
7 0 47 control 0.0682 0
8 0 41 treatment 0.418 0
9 0 47 control 0.0682 0
10 0 51 control 0.0512 0
# ... with 93 more rowsConfusion matrix
The model got \(71+8=79\) observations right out of \(71+4+20+8=103\); so its accuracy is
\[ \frac{79}{103} \approx 77\% \]
To estimate the prediction accuracy on new data, simply use the holdout method or cross-validation.
Model selection
AIC, BIC (not adjusted-\(R^2\))
the holdout method using prediction accuracy (not RMSE)
cross-validation using prediction accuracy (not RMSE)
AIC and BIC
With AIC and BIC, lower is better!
\[ AIC = 2p - \text{Goodness of fit}, \qquad BIC = p\ln(n) - \text{Goodness of fit} \]
Group exercise - model comparison with AIC
Go back to the two models you fitted for exercise 9.3. What are their respective AIC? Which model is better?
Similarly, compare the AIC of the simple (age) and multiple (age + implant) logistic regression models for the heart transplant study. Which model is better?
Group exercise - stepwise model selection with AIC
Exercise 9.7