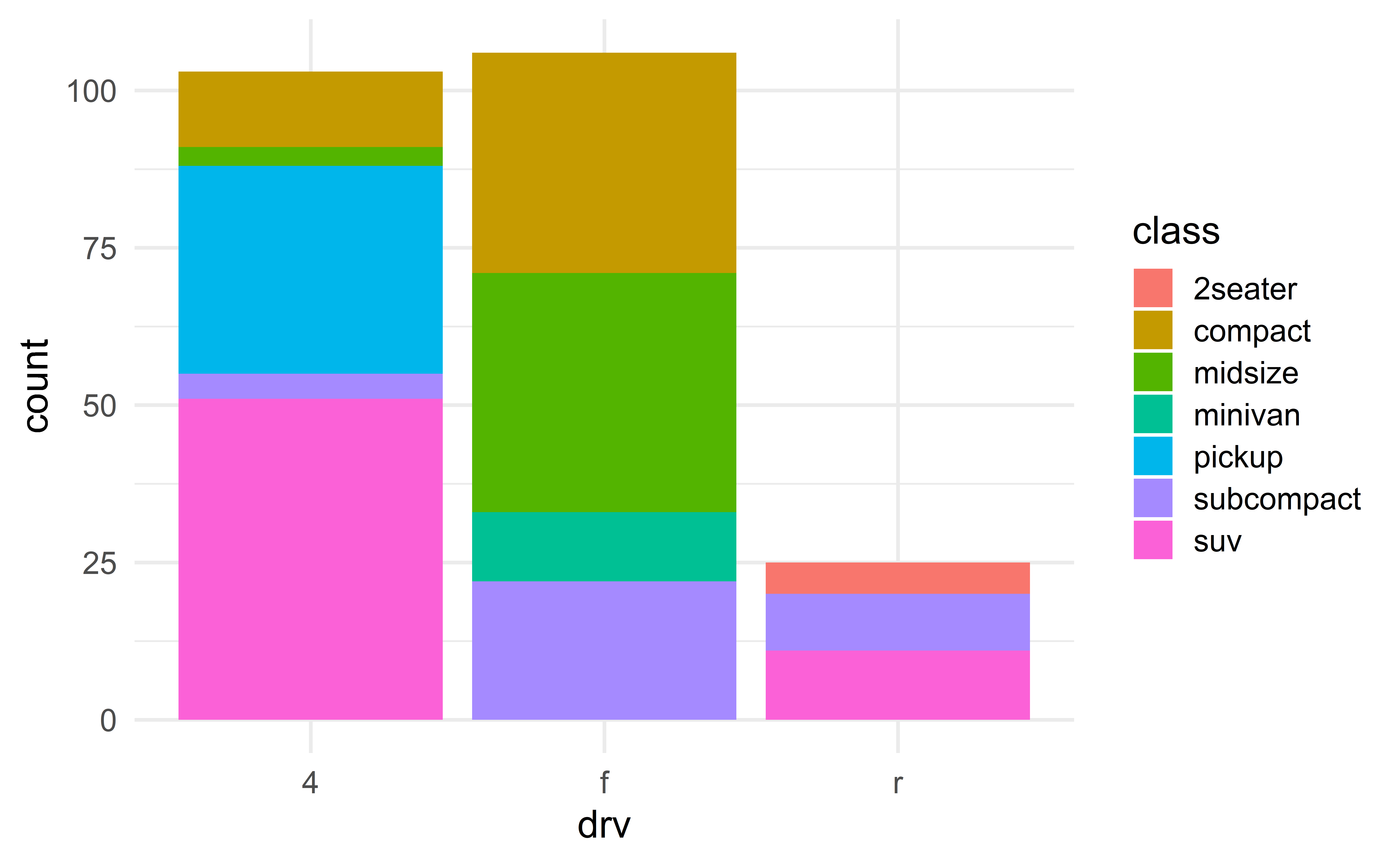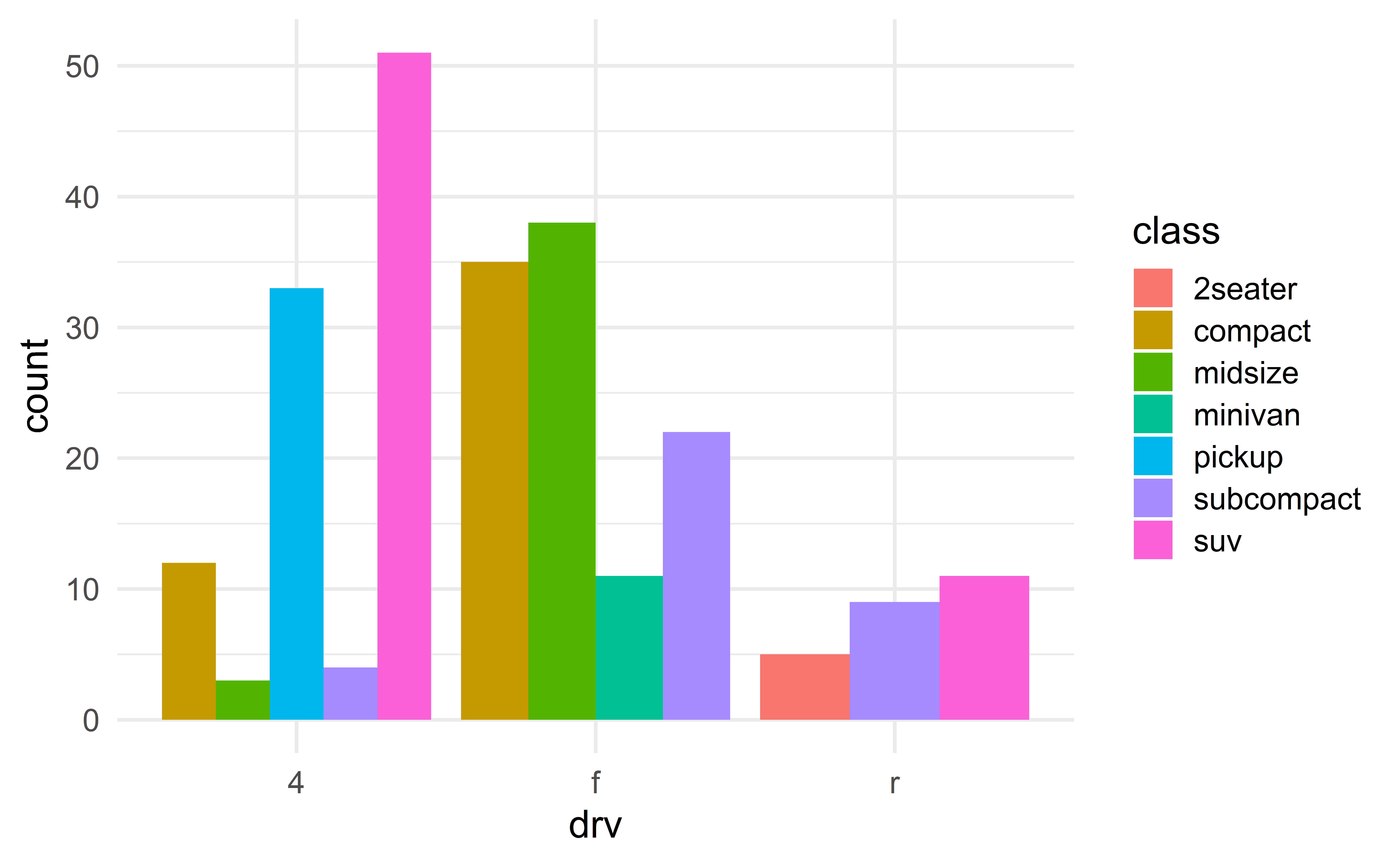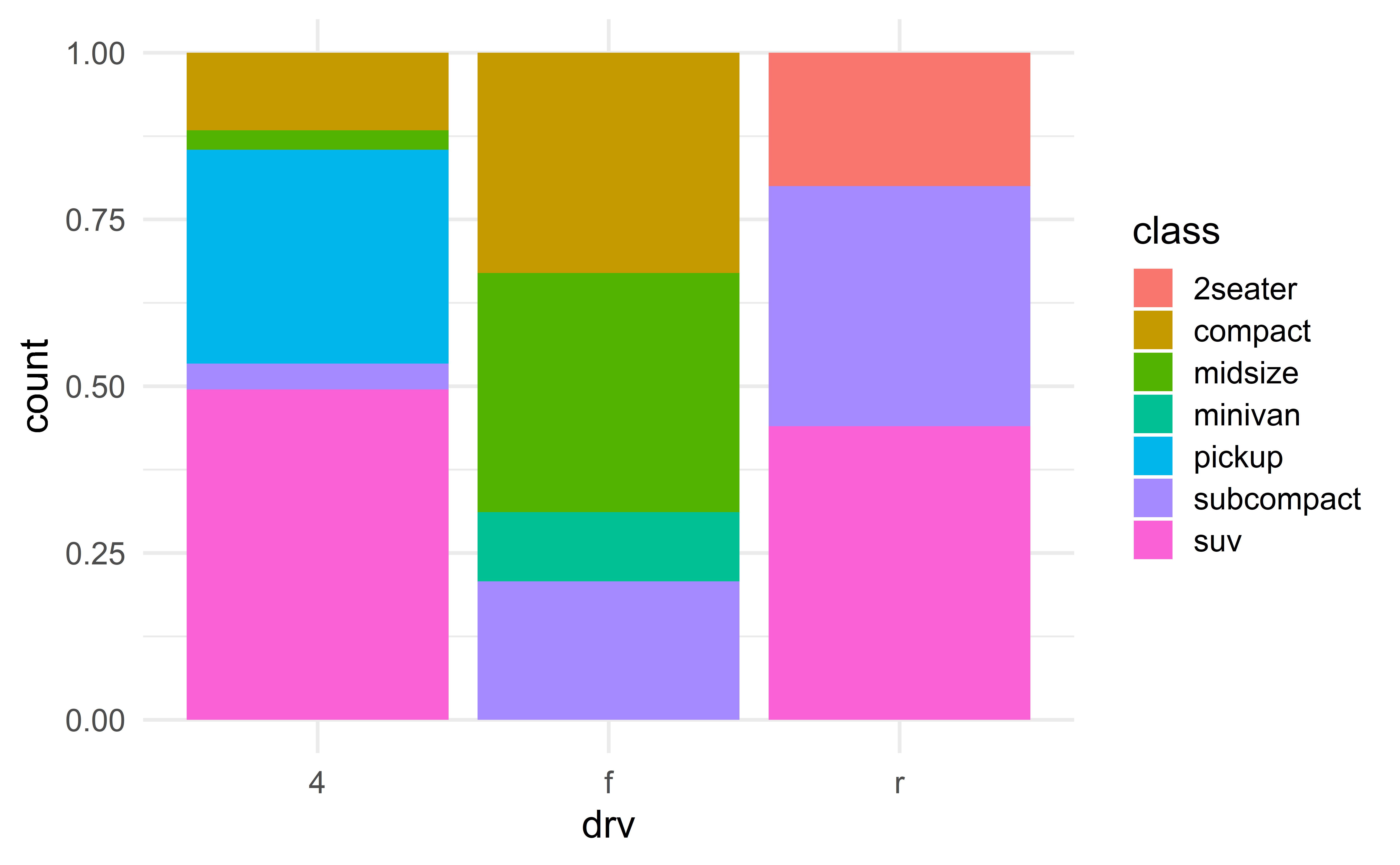Data Summary and Visualization

STA 101L - Summer I 2022

Raphael Morsomme

Welcome

Announcements - OH

• OH:
  • Raphael: Mon, Wed 10-11am (virtual)
  • Roy: Wed, Fri 4:45-5:45pm (hybrid)
• This week (exceptional):
  • Roy: Fri 2:30-3:30pm (hybrid)
  • Raphael: Sun 9:00-10:00am (virtual)

Announcements - HW

• HW due on Sunday 9:00pm and Wednesday 9:00pm
• HW 1 is due Sunday, May 15 at 9:00pm

Announcements - general

• Lectures will closely follow IMS, but
  • some topics will be skipped, e.g. 2.1.5, dot plots, etc.
  • some topics will be added, e.g. AIC and BIC
• Drop/Add for Term 1 ends tomorrow (Friday, May 13).

Franklin (albino) and Gillman have read the syllabus. Have you?

Recap of last lecture

• observations (row) and variables (column)
• population parameters and sample statistics
• statistical inference
• sampling
• four types of variables
• experiments, observational studies and causal claims

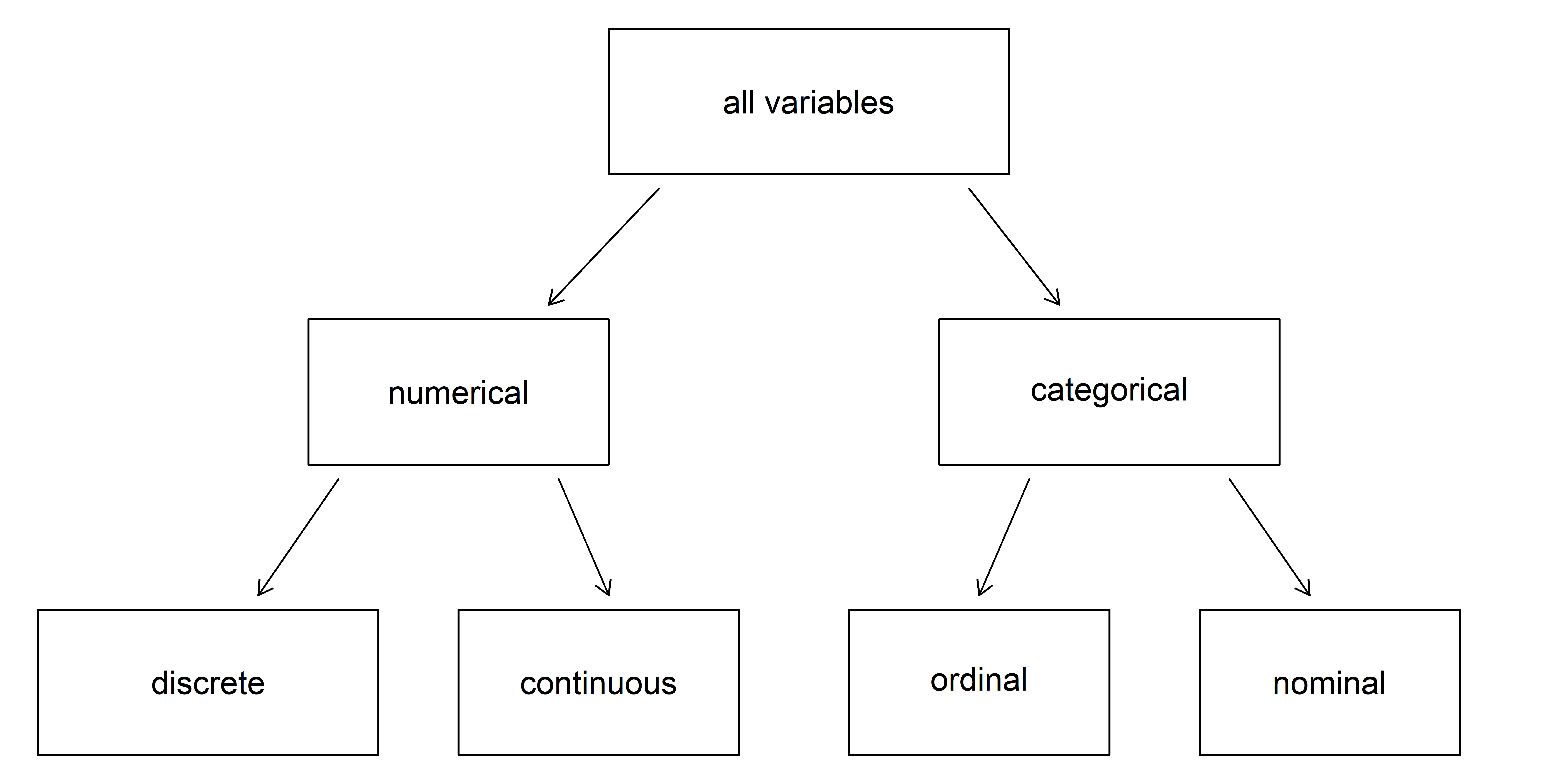
Breakdown of variables into their respective types.

Source: IMS

Outline

• Visualization for numerical data
• Summary for numerical data
• Visualization for categorical data
• Summary for categorical data
• More visualizations

“The greatest value of a picture is when it forces us to notice what we never expected to see.” — John Tukey

7 Billion: Are You Typical?

National Geographic

Group exercise - data summaries?

1. What variables are mentioned in the video?
2. What are their types?
3. How were they summarized and/or visualized?

02:00

Visualization for numerical data

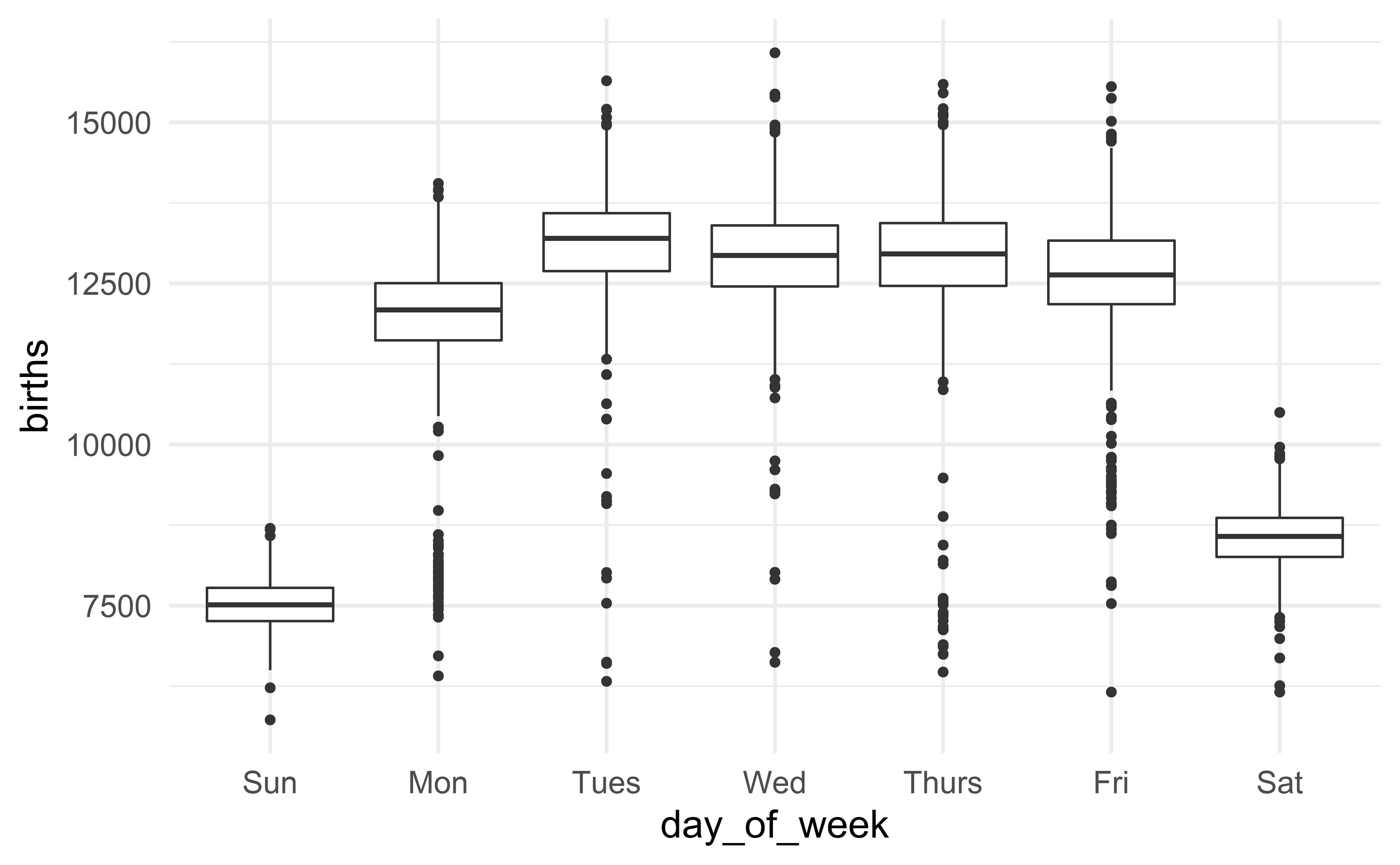
US birth data

library(fivethirtyeight) # for the USbirth dataset
d_birth <- fivethirtyeight::US_births_2000_2014

There are 5479 observations (rows)

nrow(d_birth) # number of rows

[1] 5479

and 6 variables (columns)

ncol(d_birth) # number of columns

[1] 6

head(d_birth)

# A tibble: 6 x 6
   year month date_of_month date       day_of_week births
  <int> <int>         <int> <date>     <ord>        <int>
1  2000     1             1 2000-01-01 Sat           9083
2  2000     1             2 2000-01-02 Sun           8006
3  2000     1             3 2000-01-03 Mon          11363
4  2000     1             4 2000-01-04 Tues         13032
5  2000     1             5 2000-01-05 Wed          12558
6  2000     1             6 2000-01-06 Thurs        12466

library(tidyverse)       # for data wrangling
glimpse(d_birth)

Rows: 5,479
Columns: 6
$ year          <int> 2000, 2000, 2000, 2000, 2000, 2000, 2000, 2000, 2000, 20~
$ month         <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,~
$ date_of_month <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 1~
$ date          <date> 2000-01-01, 2000-01-02, 2000-01-03, 2000-01-04, 2000-01~
$ day_of_week   <ord> Sat, Sun, Mon, Tues, Wed, Thurs, Fri, Sat, Sun, Mon, Tue~
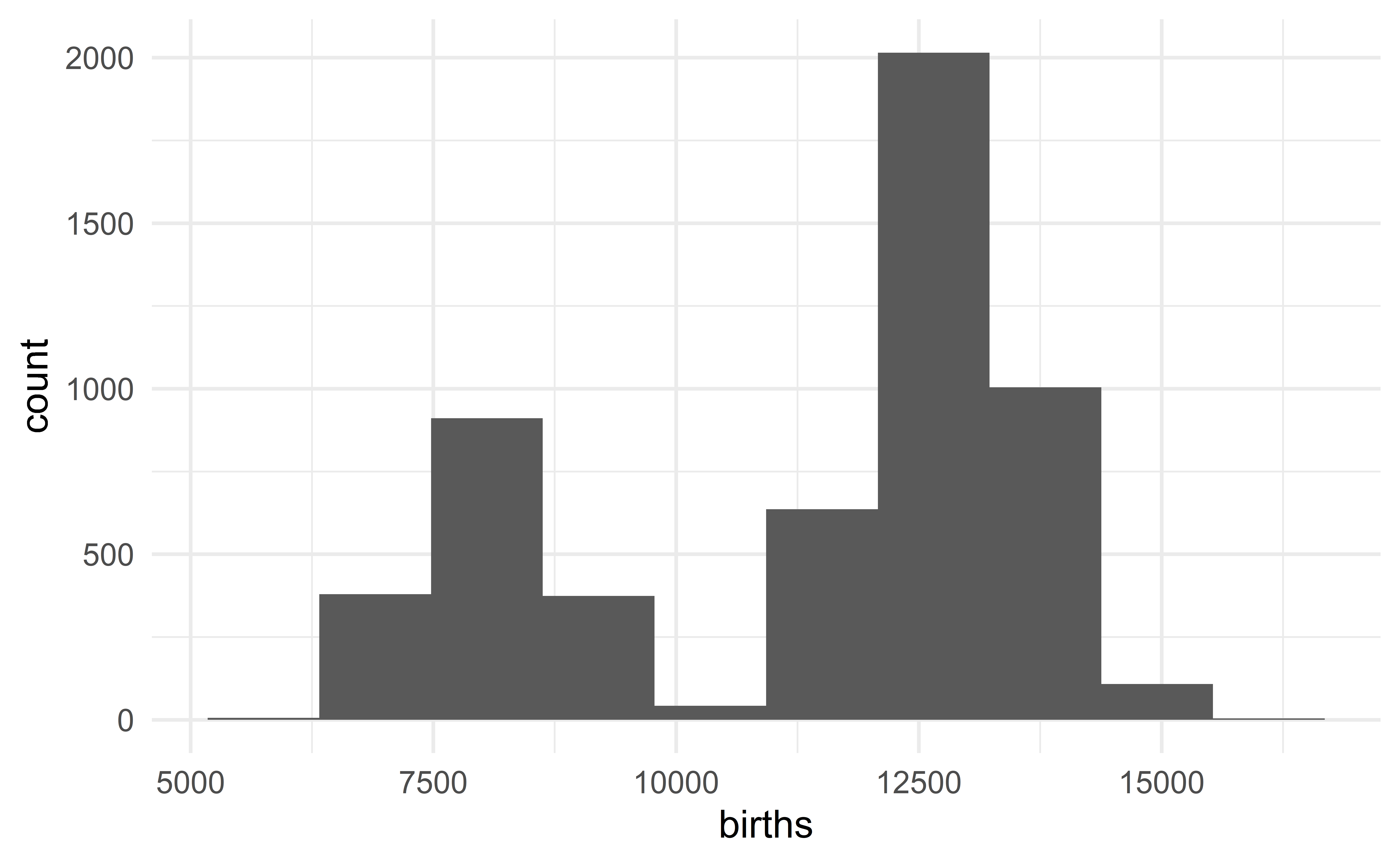
$ births        <int> 9083, 8006, 11363, 13032, 12558, 12466, 12516, 8934, 794~

Histogram

ggplot(d_birth) +
  geom_histogram(aes(births)) +
  labs(title = "Daily number of natural births in the US between 2000 and 2014")

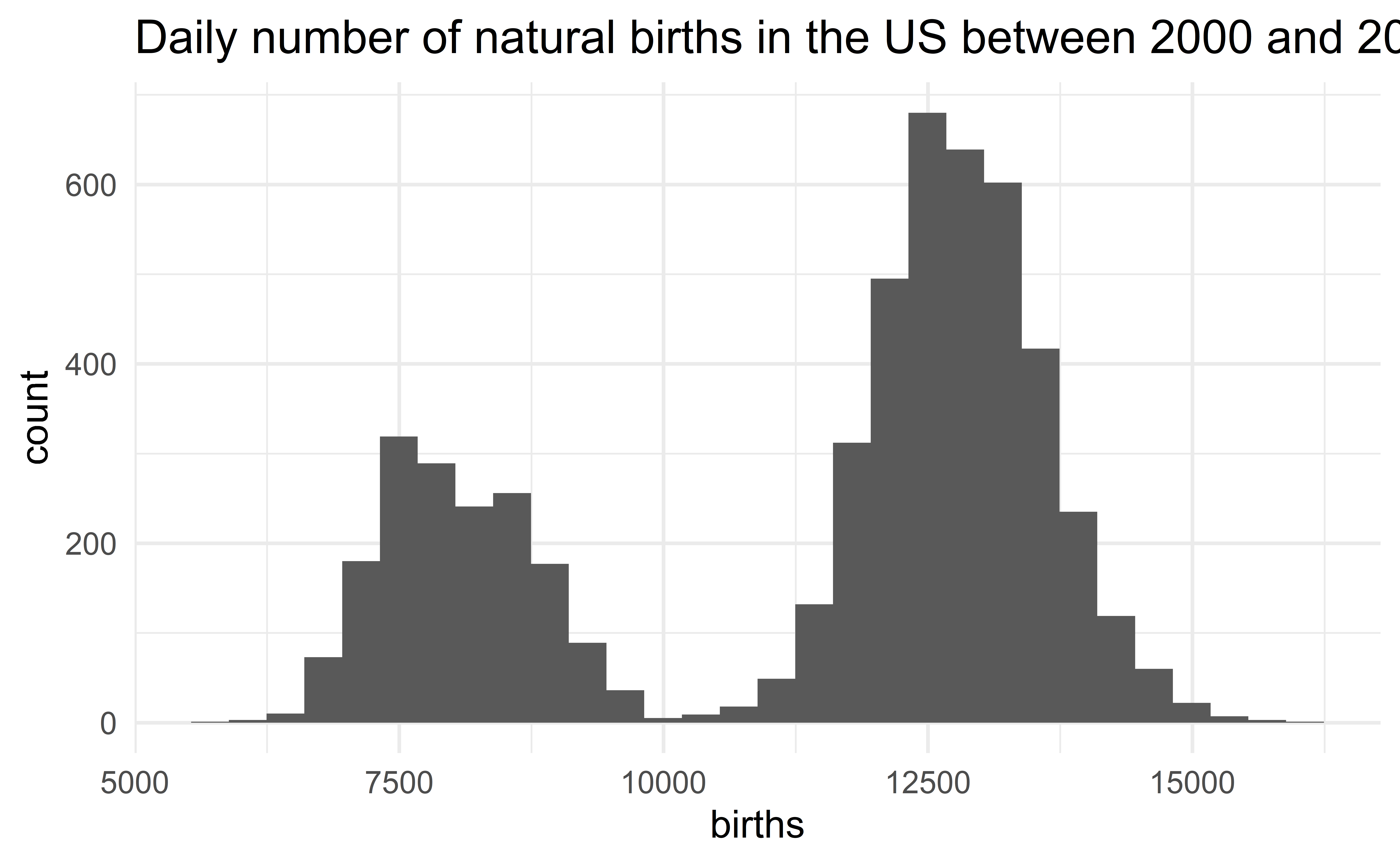
• Higher bars indicate where the data are relatively more common
• More days with around 8,000 births or with around 12,500 births
• Few days with less than 7,000 or more than 14,000 births.
• Also few days with around 10,000 births

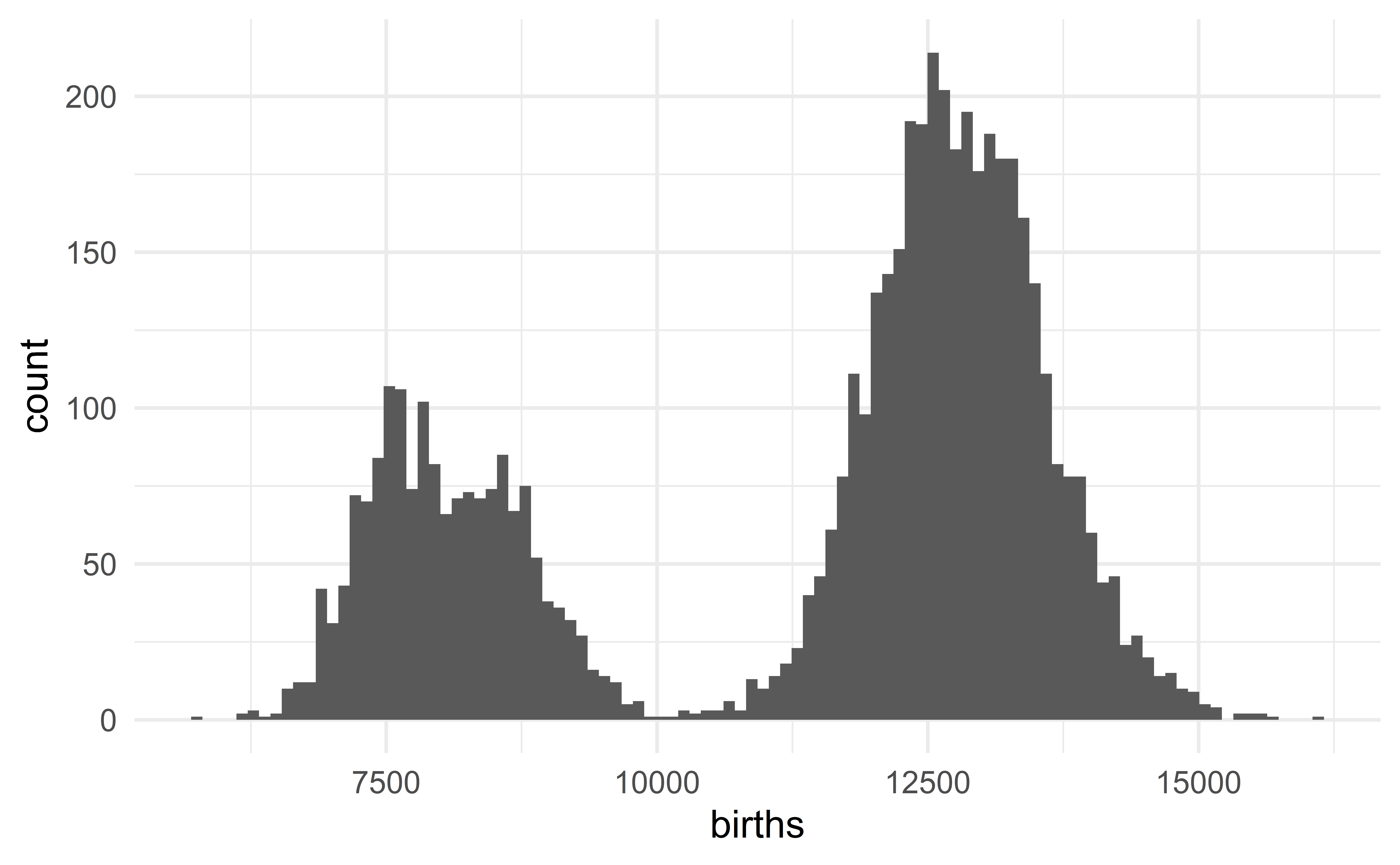
We can change the number of bins to have a rougher or more detailed histogram.

• bins = 10
• bins = 100

ggplot(d_birth) +
  geom_histogram(aes(births), bins = 10)

ggplot(d_birth) +
  geom_histogram(aes(births), bins = 100)

Statistics as an art - describing a distribution

Tip

To explore a numerical variable, always start with a histogram

To describe the distribution of a numerical variable, we comment on

• the mode(s): unimodal, bimodal, multimodal
• the shape of each mode: flat, bell-shape, bounded
• the symmetry: symmetric, left skewed, right skewed
• the outliers: presence of extreme values
• any other surprising feature.

Describing a distribution is an art

Note that some distributions will not fit nicely in these categories.

Describing the US birth data

The distribution of the daily number of births in the US is bimodal with each mode being bell-shaped and symmetric. We observe no extreme value.

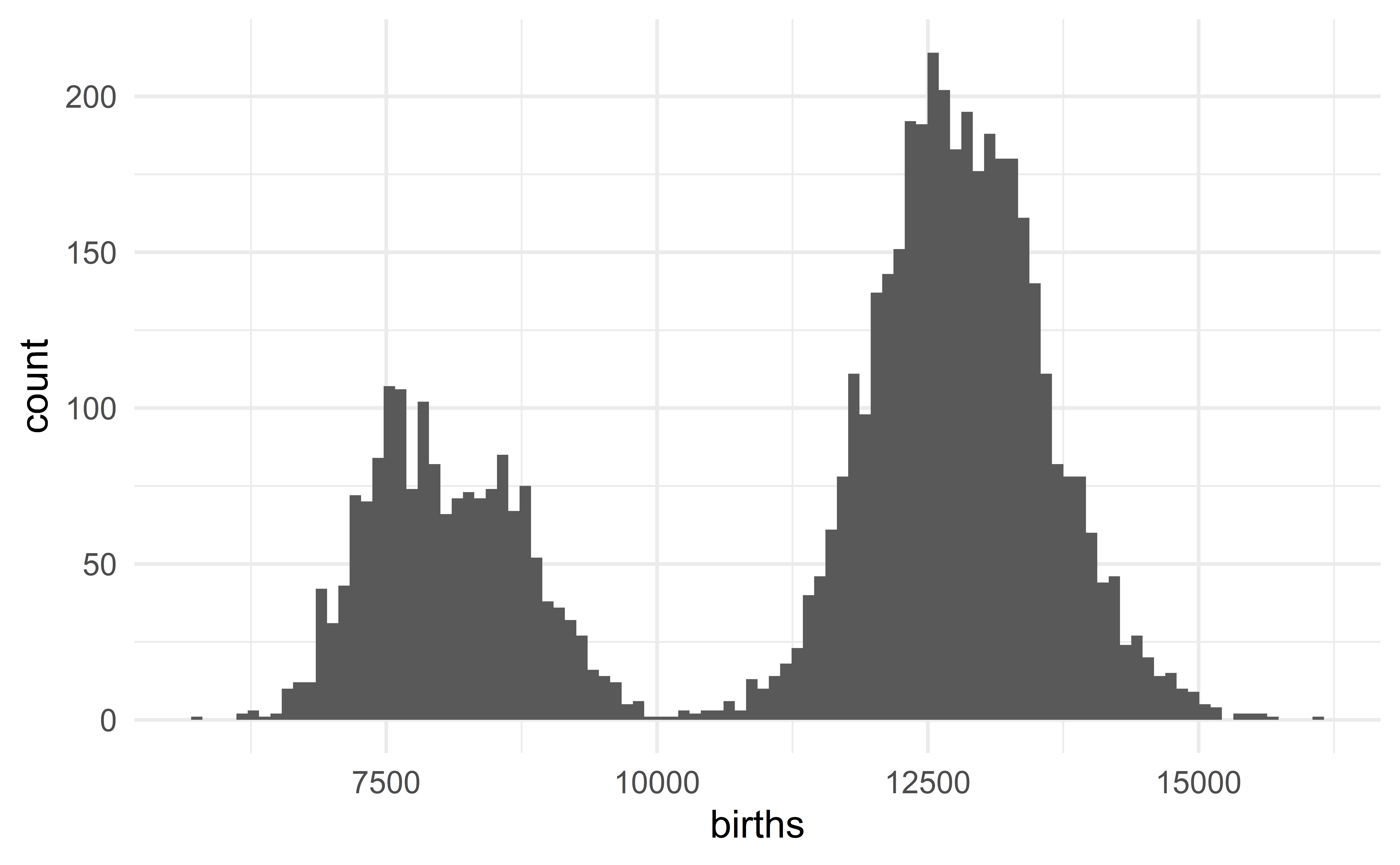
Group exercise - describing a distribution

Describe the distributions in exercises 5.6, 5.13, 5.24 and 5.26 (only consider the histograms)

04:00

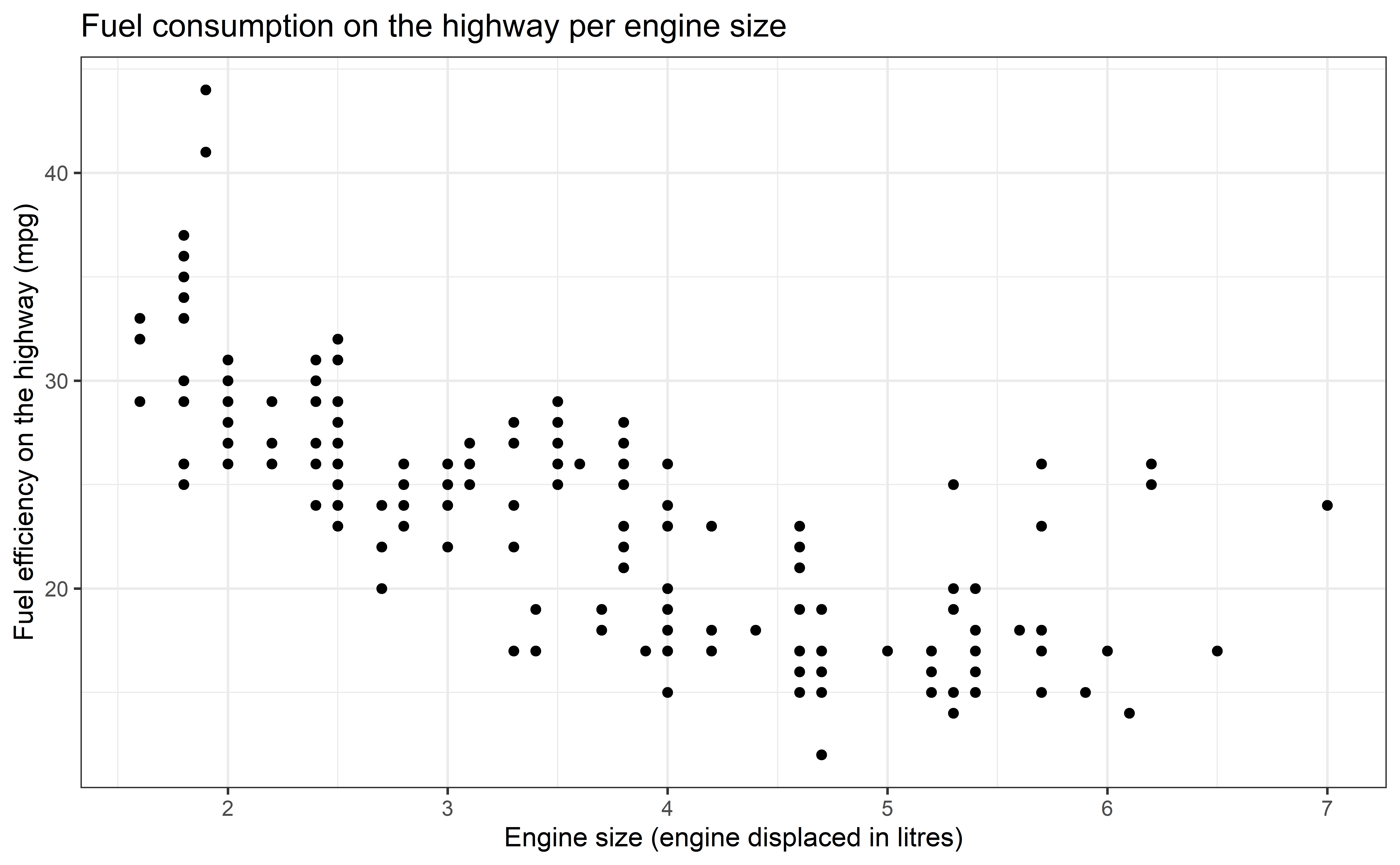
Scatterplots

Histograms: visualize the distribution of a single numerical variable.

Scatterplots: visualize the relation between two numerical variables.

The mpg dataset

d_car <- ggplot2::mpg
head(d_car)

# A tibble: 6 x 11
  manufacturer model displ  year   cyl trans      drv     cty   hwy fl    class 
  <chr>        <chr> <dbl> <int> <int> <chr>      <chr> <int> <int> <chr> <chr> 
1 audi         a4      1.8  1999     4 auto(l5)   f        18    29 p     compa~
2 audi         a4      1.8  1999     4 manual(m5) f        21    29 p     compa~
3 audi         a4      2    2008     4 manual(m6) f        20    31 p     compa~
4 audi         a4      2    2008     4 auto(av)   f        21    30 p     compa~
5 audi         a4      2.8  1999     6 auto(l5)   f        16    26 p     compa~
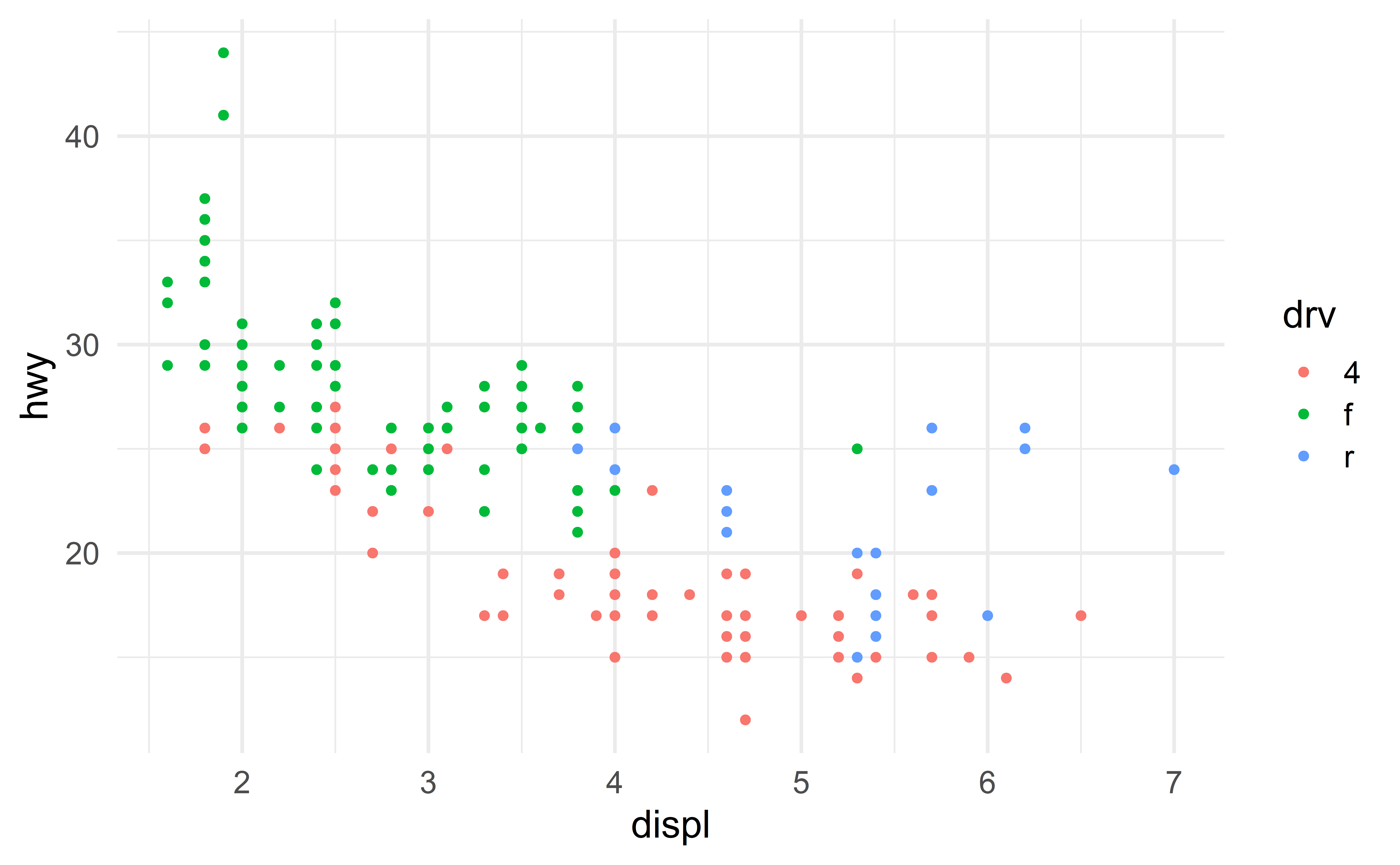
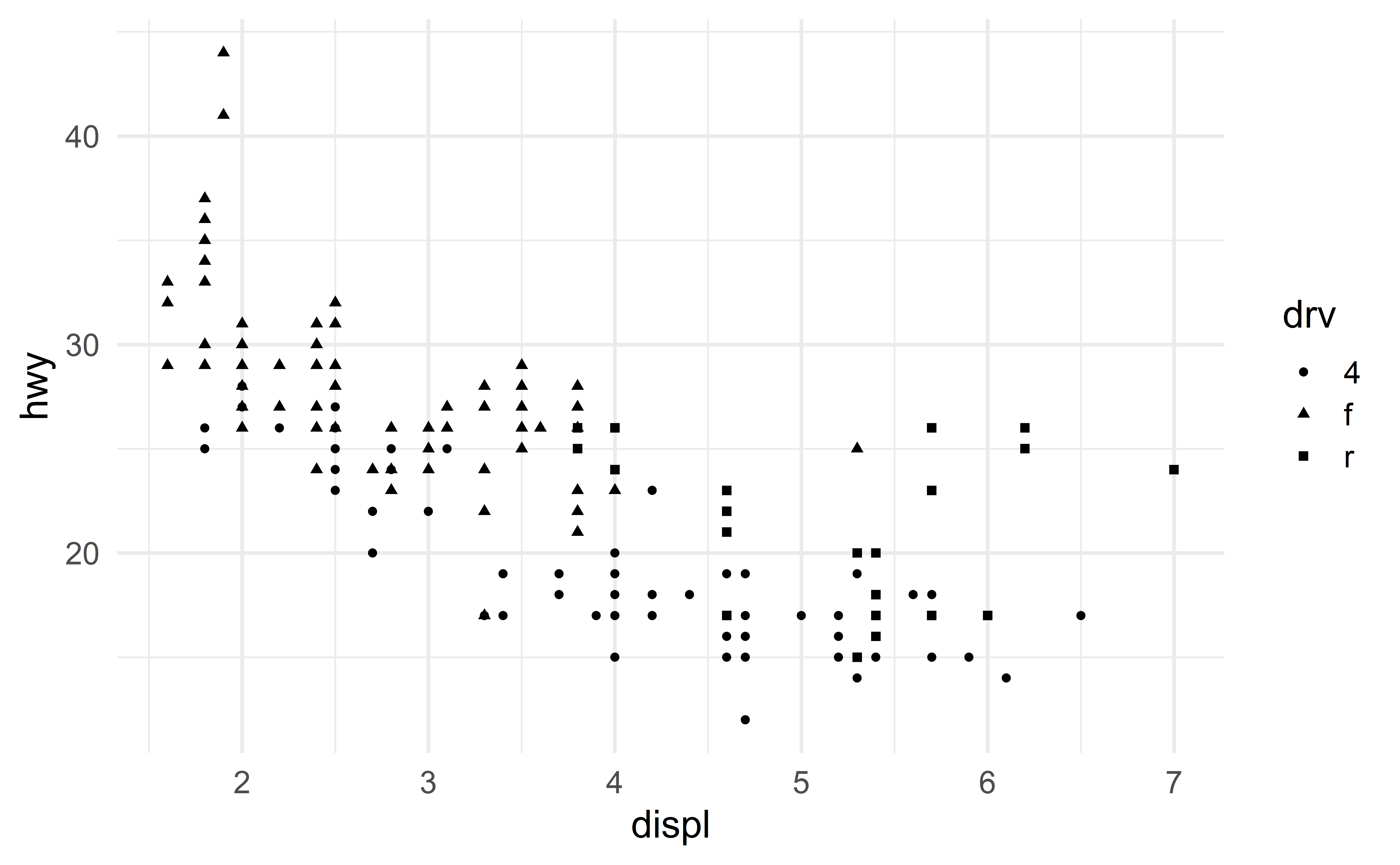
6 audi         a4      2.8  1999     6 manual(m5) f        18    26 p     compa~

We will look at the relation between engine size (disp) and fuel efficiency (hwy).

ggplot(d_car) +
  geom_point(aes(displ, hwy)) +
  labs(title = "Relation between fuel consumption on the highway and engine size")

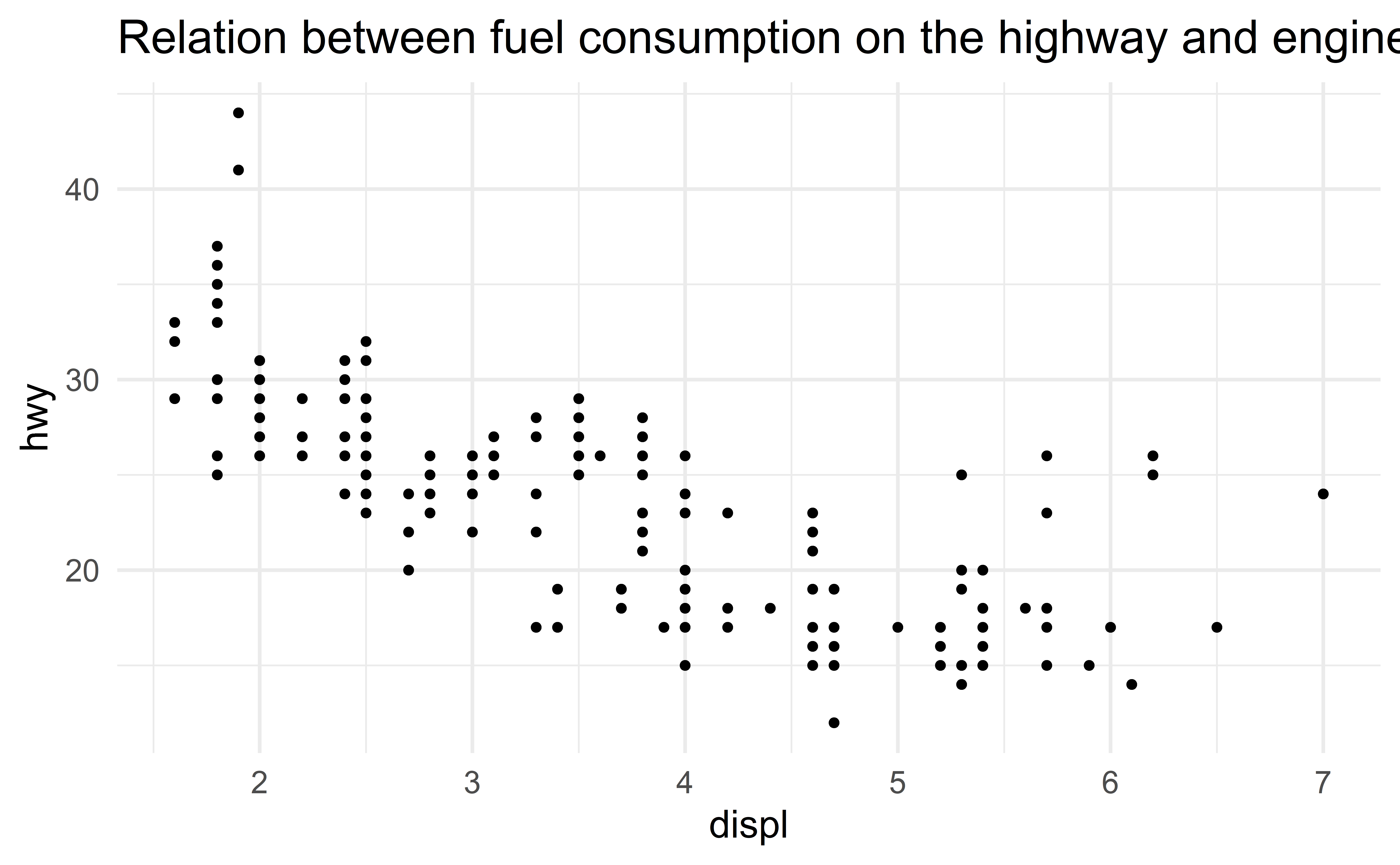
Note

To add an additional variable to your visualization, you can use color or symbols.

• Colored points
• Symbols

ggplot(d_car) +
  geom_point(aes(displ, hwy, col = drv))

ggplot(d_car) +
  geom_point(aes(displ, hwy, shape = drv))

Summary for numerical data

Measures of centrality

• The average: \(\bar{x} = \dfrac{x_1 + \dots + x_n}{n}\)
  • To compute the average age in the class, we would calculate

\[ \overline{\text{age}} = \dfrac{\text{age}_{Hayden} + \text{age}_{Janice} + \text{age}_{Kenndy} + \text{age}_{Maggie} + \text{age}_{Melissa} + \text{age}_{Yuanzhi}}{6} \]

• The median: the middle value
  • 50% of the sample is large than the median, and 50% is smaller.

mean(d_birth$births)   # average

[1] 11350.07

median(d_birth$births) # median

[1] 12343

Percentiles

Percentiles are a generalization of the median.

The value that is larger than p% of the data and smaller than the rest is called the p-th percentile.

The median is the 50th percentile.

We will soon make use of the 25th and 75th percentiles.

Later in the course, the 95th and 97.5th percentiles will also be useful.

Measures of variation

• Variance: average squared distance from the mean
  • Standard deviation (sd): square root of the variance (roughly speaking, the average distance to the mean)
  • Most (+- 95%) of the data is within 2 sd of the mean.
• Inter-quartile range (IQR): distance between the 25th and the 75th percentiles.

var(d_birth$births) # variance

[1] 5409444

sd(d_birth$births) # sd

[1] 2325.821

IQR(d_birth$births) # iqr

[1] 4342

Robustness

Real-world data often contain extreme values

• measurement errors,
• typos,
• extreme observations,
• …

The average, median, variance, sd and iqr are not equally robust to the presence of extreme values.

Let us contaminate the birth data with an extreme value of 1 billion…

x_uncontaminated <- d_birth$births  
x_contaminated   <- c(x_uncontaminated, 1e9) # 1e9 = 10^9 (scientific notation)

…and compare the mean, median, variance, sd and iqr of these two variables.

summary(x_uncontaminated)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   5728    8740   12343   11350   13082   16081 

summary(x_contaminated)

     Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
5.728e+03 8.740e+03 1.234e+04 1.938e+05 1.308e+04 1.000e+09 

var(x_uncontaminated); var(x_contaminated)

[1] 5409444

[1] 1.824776e+14

sd(x_uncontaminated); sd(x_contaminated)

[1] 2325.821

[1] 13508428

IQR(x_uncontaminated); IQR(x_contaminated)

[1] 4342

[1] 4342.25

Robustness of the median and the iqr

While the median and iqr are robust to the presence of extreme values, the mean, variance and sd are not.

Group exercise - summary statistics

Exercises 5.8, 5.11, 5.15 (replace part \(c\) by height of all adults)

Bonus: 5.17, 5.19

Note: Q1 is first the 25th percentile (larger than one quarter of the data), Q3 is the 75th percentile.

05:00

Summary for categorical data

Frequency table (1d)

head(d_car)

# A tibble: 6 x 11
  manufacturer model displ  year   cyl trans      drv     cty   hwy fl    class 
  <chr>        <chr> <dbl> <int> <int> <chr>      <chr> <int> <int> <chr> <chr> 
1 audi         a4      1.8  1999     4 auto(l5)   f        18    29 p     compa~
2 audi         a4      1.8  1999     4 manual(m5) f        21    29 p     compa~
3 audi         a4      2    2008     4 manual(m6) f        20    31 p     compa~
4 audi         a4      2    2008     4 auto(av)   f        21    30 p     compa~
5 audi         a4      2.8  1999     6 auto(l5)   f        16    26 p     compa~
6 audi         a4      2.8  1999     6 manual(m5) f        18    26 p     compa~

table(d_car$drv)

  4   f   r 
103 106  25 

Contigency table (2d)

table(d_car$class, d_car$drv)

            
              4  f  r
  2seater     0  0  5
  compact    12 35  0
  midsize     3 38  0
  minivan     0 11  0
  pickup     33  0  0
  subcompact  4 22  9
  suv        51  0 11

Proportion table (2d)

• table proportion
• row proportion
• column proportion

table(d_car$class, d_car$drv) %>%
  prop.table() %>%
  round(2)

            
                4    f    r
  2seater    0.00 0.00 0.02
  compact    0.05 0.15 0.00
  midsize    0.01 0.16 0.00
  minivan    0.00 0.05 0.00
  pickup     0.14 0.00 0.00
  subcompact 0.02 0.09 0.04
  suv        0.22 0.00 0.05

table(d_car$class, d_car$drv) %>%
  prop.table(1) %>%
  round(2)

            
                4    f    r
  2seater    0.00 0.00 1.00
  compact    0.26 0.74 0.00
  midsize    0.07 0.93 0.00
  minivan    0.00 1.00 0.00
  pickup     1.00 0.00 0.00
  subcompact 0.11 0.63 0.26
  suv        0.82 0.00 0.18

table(d_car$class, d_car$drv) %>%
  prop.table(2) %>%
  round(2)

            
                4    f    r
  2seater    0.00 0.00 0.20
  compact    0.12 0.33 0.00
  midsize    0.03 0.36 0.00
  minivan    0.00 0.10 0.00
  pickup     0.32 0.00 0.00
  subcompact 0.04 0.21 0.36
  suv        0.50 0.00 0.44

Group exercise - contigency and proportion table

1. What does the number \(12\) (2nd row, 1st column) represent in the contigency table?
2. What does the number \(0.05\) (2nd row, 1st column) represent in the first proportion table?
3. What does the number \(0.25\) (2nd row, 1st column) represent in the row proportion table?

03:00

Visualization for categorical data

Barplot

ggplot(d_car) +
  geom_bar(aes(drv))

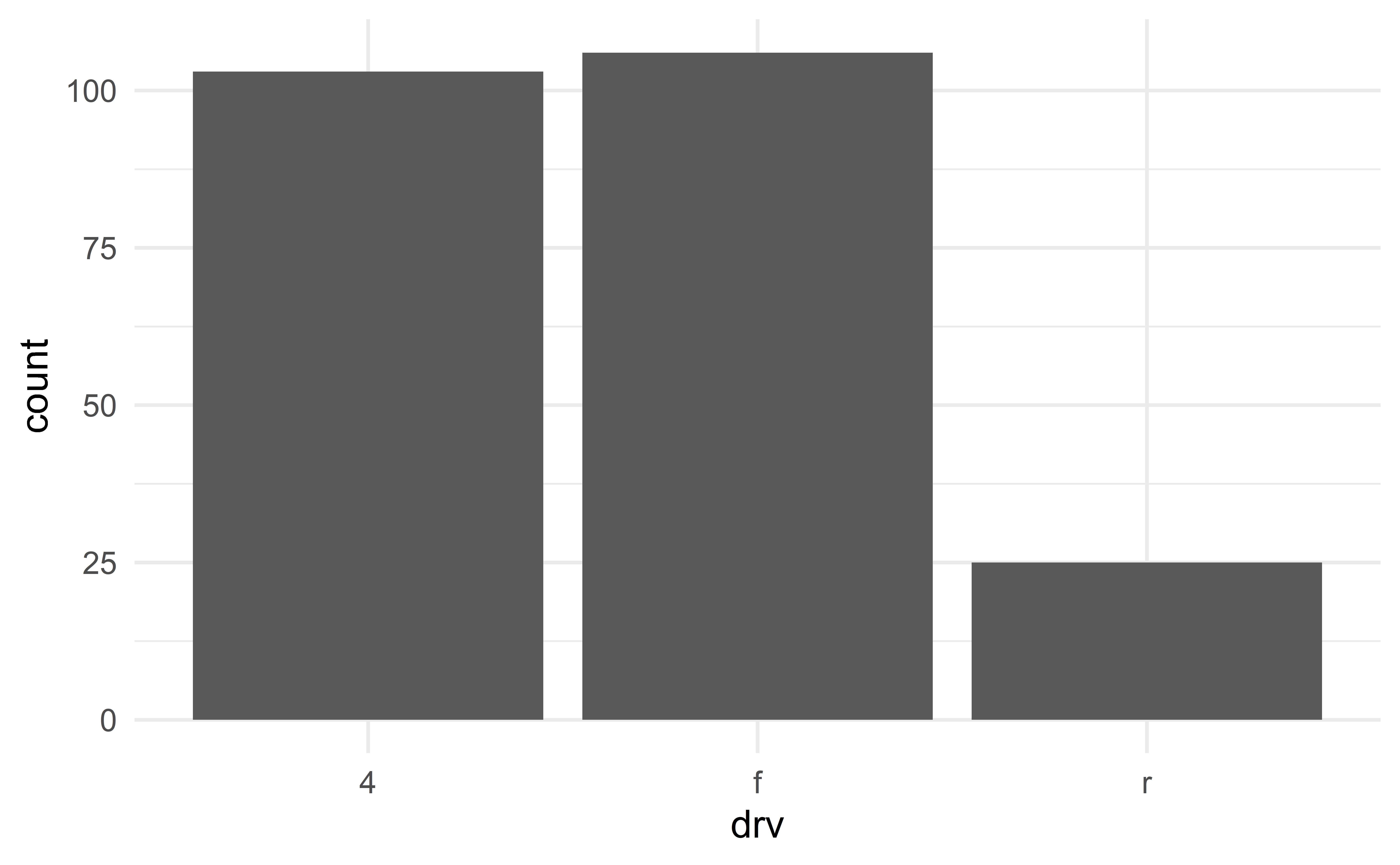
We can add a second categorical variable using colors.

Advanced barplots

• stacked
• dodged
• standardized

ggplot(d_car) +
  geom_bar(aes(drv, fill = class))

ggplot(d_car) +
  geom_bar(aes(drv, fill = class), position = "dodge")

ggplot(d_car) +
  geom_bar(aes(drv, fill = class), position = "fill")

Group exercise - pros and cons of barplots

Exercise 4.5

03:00

Advanced visualizations

Faceted histograms

d_birth_small <- filter(d_birth, year %in% c(2000, 2004, 2009, 2014))
ggplot(d_birth_small) +
  geom_histogram(aes(births)) + 
  facet_grid(year~.)

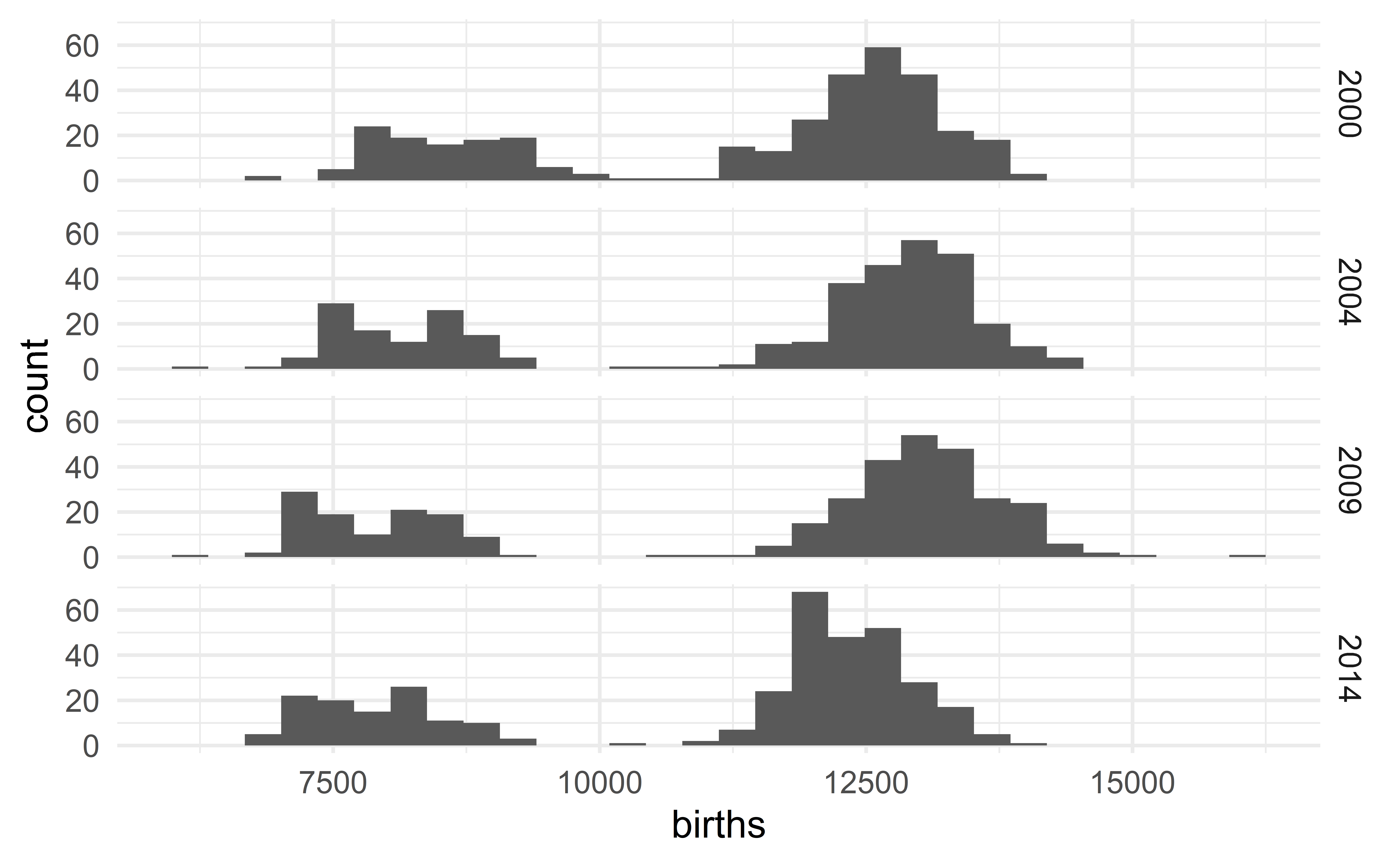
Beyond 2 variables

Faceted figures are a great way to include \(\ge\) 3 variables! See exercise 1.13

Mosaic plot

ggplot(d_car) +
  geom_mosaic(aes(x = product(drv), fill = class))

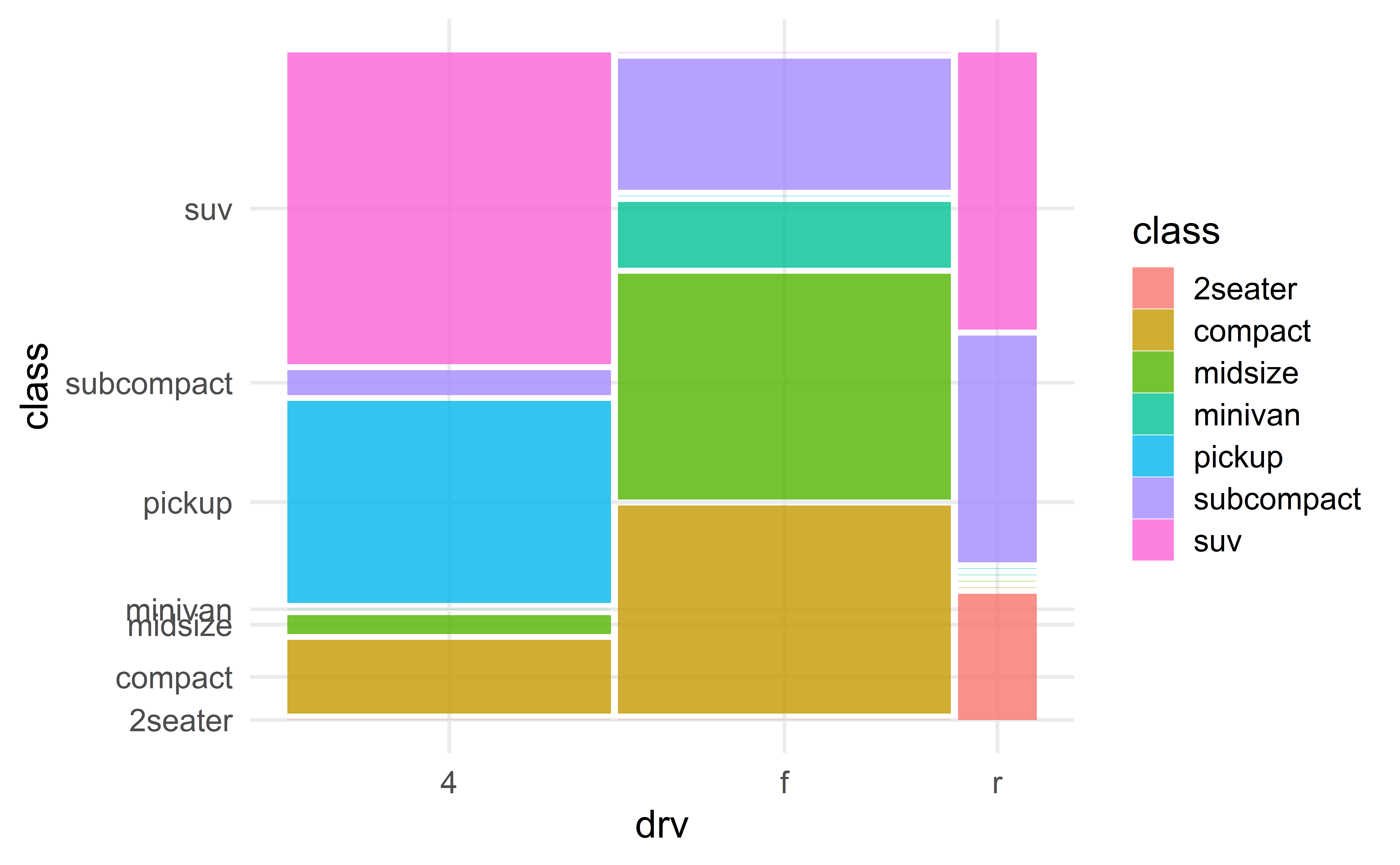
✅ Combines the strengths of the various barplots.

🛑 Not in the tool box of every data scientist

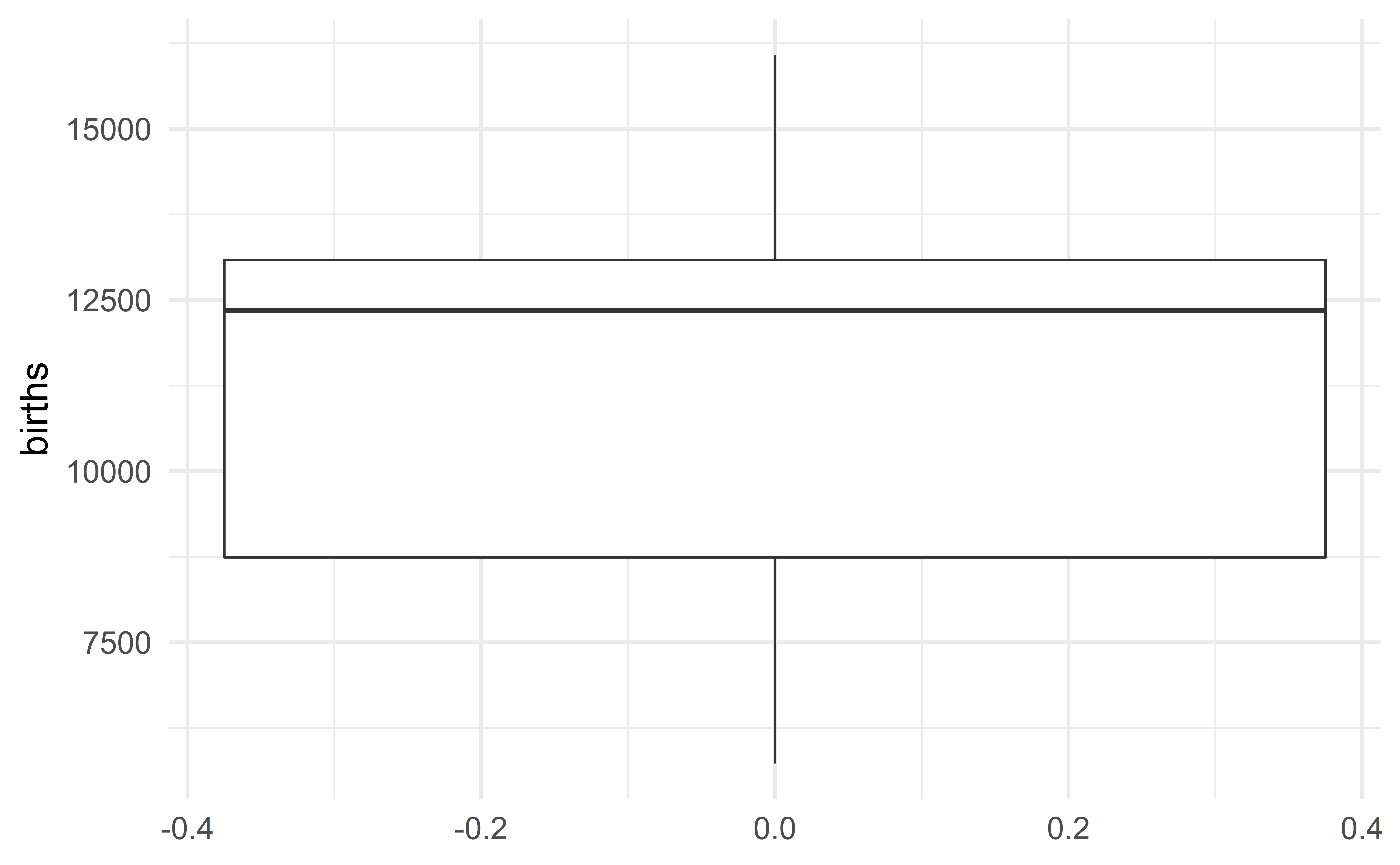
Boxplots

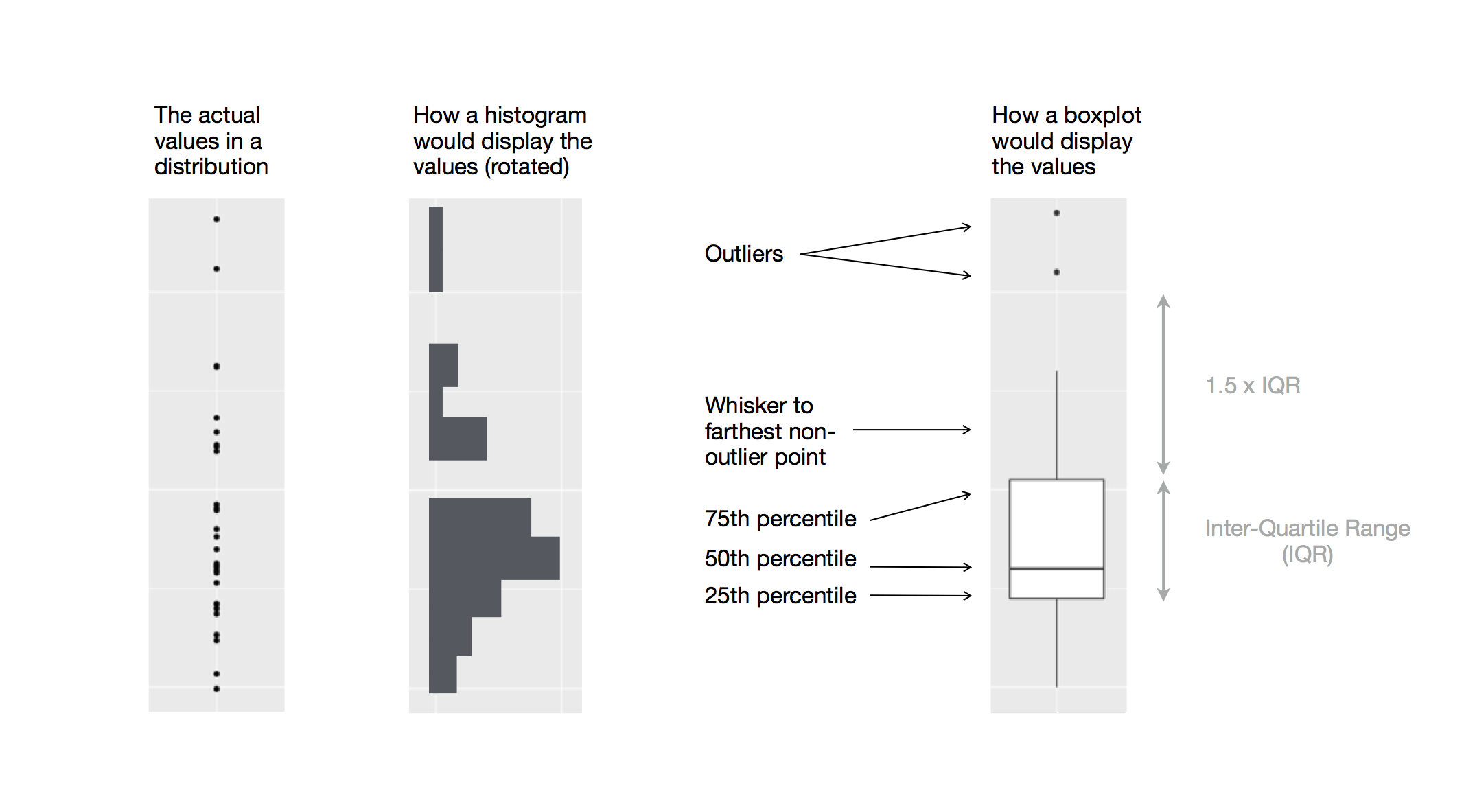
From raw data to boxplot

Source: R 4 Data Science

• The thick line in the middle of the box indicates the median;

• the box stretches from the 25th percentile (Q1) to the 75th percentile (Q3); it covers 50% of the data;

• the length of the whiskers are at most 1.5 iqr;

• any observation more than 1.5 iqr away from the box is labelled as an outlier;

• more compact than histograms

Outliers

Outliers have an extreme value. How to deal with an outlier depends on why the observation stands out. Outliers can be

• removed
• corrected
• ignored

Group exercise - limitation of boxplots

Exercise 5.13

01:00

• Boxplot
• Side-by-side boxplots

ggplot(d_birth) +
  geom_boxplot(aes(y = births))

ggplot(d_birth) +
  geom_boxplot(aes(y=births, x=day_of_week))

Editing figures

Figure title

ggplot(d_car) +
  geom_point(aes(displ, hwy)) +
  labs(title = "Fuel consumption on the highway per engine size")

Axis labels

ggplot(d_car) +
  geom_point(aes(displ, hwy)) +
  labs(
    title = "Fuel consumption on the highway per engine size",
    x = "Engine size (engine displaced in litres)",
    y = "Fuel efficiency on the highway (mpg)"
    )

• theme_bw
• theme_classic
• theme_dark

Show the code

ggplot(d_car) +
  geom_point(aes(displ, hwy)) +
  labs(
    title = "Fuel consumption on the highway per engine size",
    x = "Engine size (engine displaced in litres)",
    y = "Fuel efficiency on the highway (mpg)"
    ) +
  theme_bw()

Show the code

ggplot(d_car) +
  geom_point(aes(displ, hwy)) +
  labs(
    title = "Fuel consumption on the highway per engine size",
    x = "Engine size (engine displaced in litres)",
    y = "Fuel efficiency on the highway (mpg)"
    ) +
  theme_classic()

Show the code

ggplot(d_car) +
  geom_point(aes(displ, hwy)) +
  labs(
    title = "Fuel consumption on the highway per engine size",
    x = "Engine size (engine displaced in litres)",
    y = "Fuel efficiency on the highway (mpg)"
    ) +
  theme_dark()

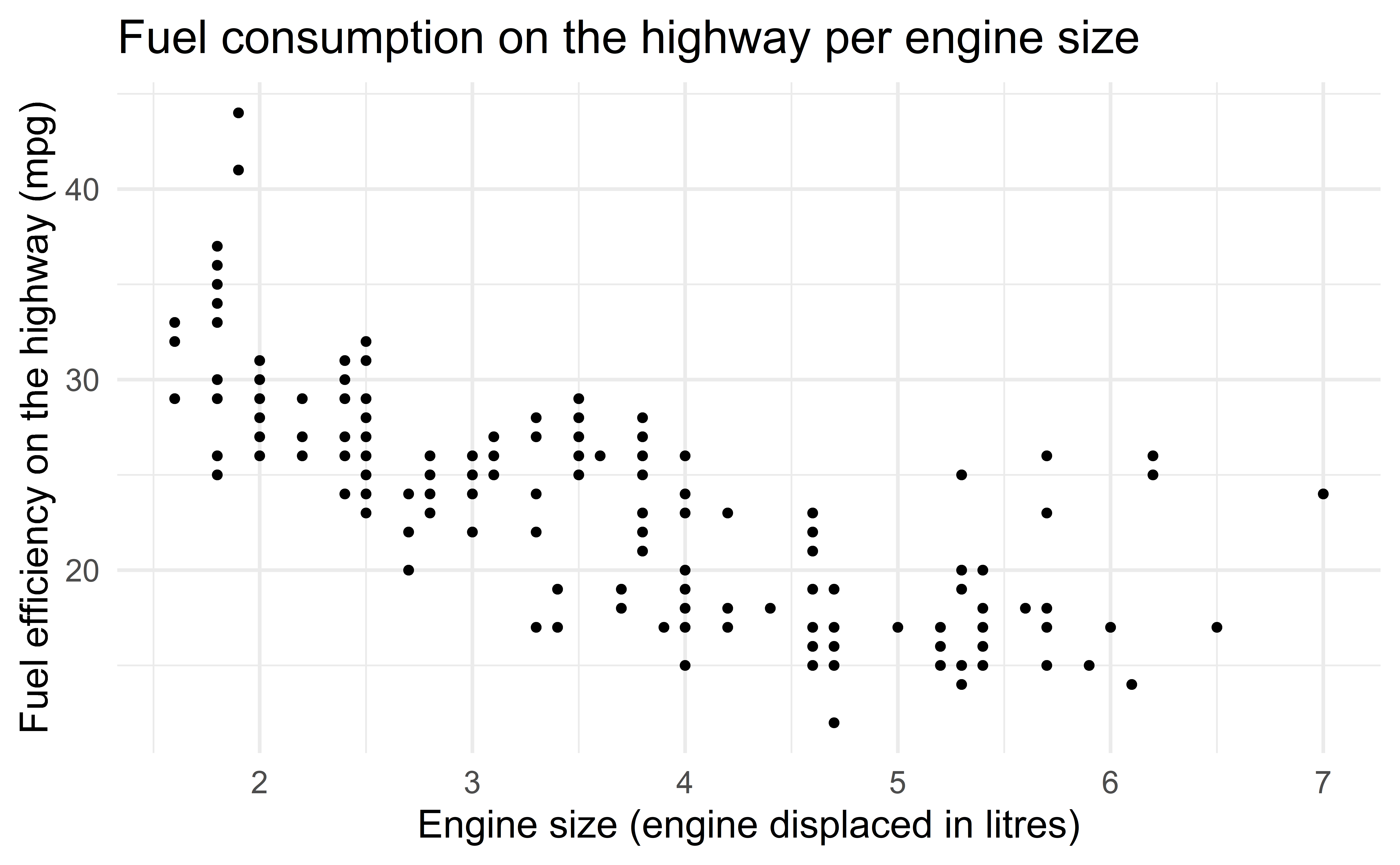
Editing tables

table(d_car$class, d_car$drv) %>%
  prop.table(1) %>%
  round(2) %>%
  kbl(caption = "Distribution of drive type per class of car") %>%
  kable_classic(full_width = FALSE, c("striped", "hover"))

Distribution of drive type per class of car

	4	f	r
2seater	0.00	0.00	1.00
compact	0.26	0.74	0.00
midsize	0.07	0.93	0.00
minivan	0.00	1.00	0.00
pickup	1.00	0.00	0.00
subcompact	0.11	0.63	0.26
suv	0.82	0.00	0.18

📋 See this vignette for more details on editing tables

Effective communication

Statistics as an art - figures

• Have a purpose: is the figure necessary?

• Parsimony: keep it simple and avoid distractions

• Tell a story: provide context and interpret the figure

• At least 3 variables as often as possible: color, shape, facets, etc.

• Edit your figure: title, axes, theme, etc.

📋 See R for Data Science - chapters 3 and 7 for more on data visualization in R.

Recap

Recap

• Histogram, scatterplot, boxplot
• Average, median, variance, sd and IQR; robustness
• Frequency, contigency and proportion tables
• Barplot, mosaic plot
• Effective communication: well-edited figures, \(\ge3\) variables (symbols, colors, facets), tell a story
• R for Data Science - chapters 3 and 7

“The simple graph has brought more information to the data analyst’s mind than any other device.” — John Tukey