Classical inference

STA 101L - Summer I 2022

Raphael Morsomme

Welcome

Announcements

  • Tuesday: lecture + QA

  • Wednesday: work on project (online OH)

  • Thursday: work on project (online OH)

  • Friday: presentations

Recap

  • HT via simulation

  • CI via bootstrap

  • 5 cases

    • one proportion

    • two proportions

    • one mean

    • two means

    • linear regression

Outline

  • Normal approximation
  • Classical approach to statistical inference
  • Standard error
  • Case 6 – many proportions (\(\chi^2\) test)
  • Case 7 – many means (ANOVA)

Individual exercise - warm up

Exercise 14.5

Exercise 17.2 – parts a and c

Exercise 17.4 – part c

03:00

Normal approximation

Normal distribution

tibble(x = seq(-5, 5, by = 0.001)) %>%
  mutate(normal = dnorm(x, mean = 0, sd = 1)) %>%
  ggplot() + 
  geom_line(aes(x, normal))

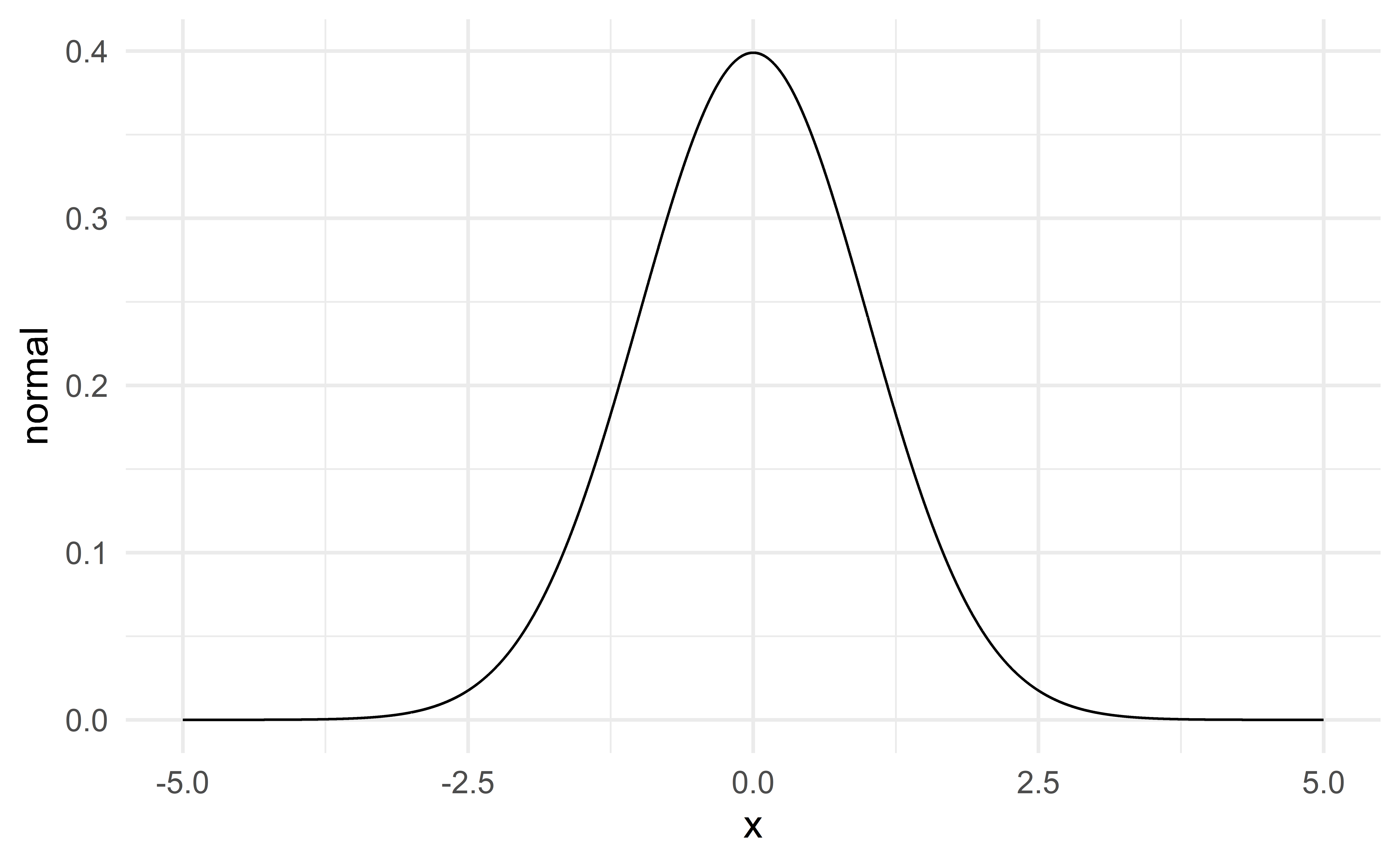
\(\Rightarrow\) unimodal, symmetric, thin tails – bell-shaped

HT using a normal approximation

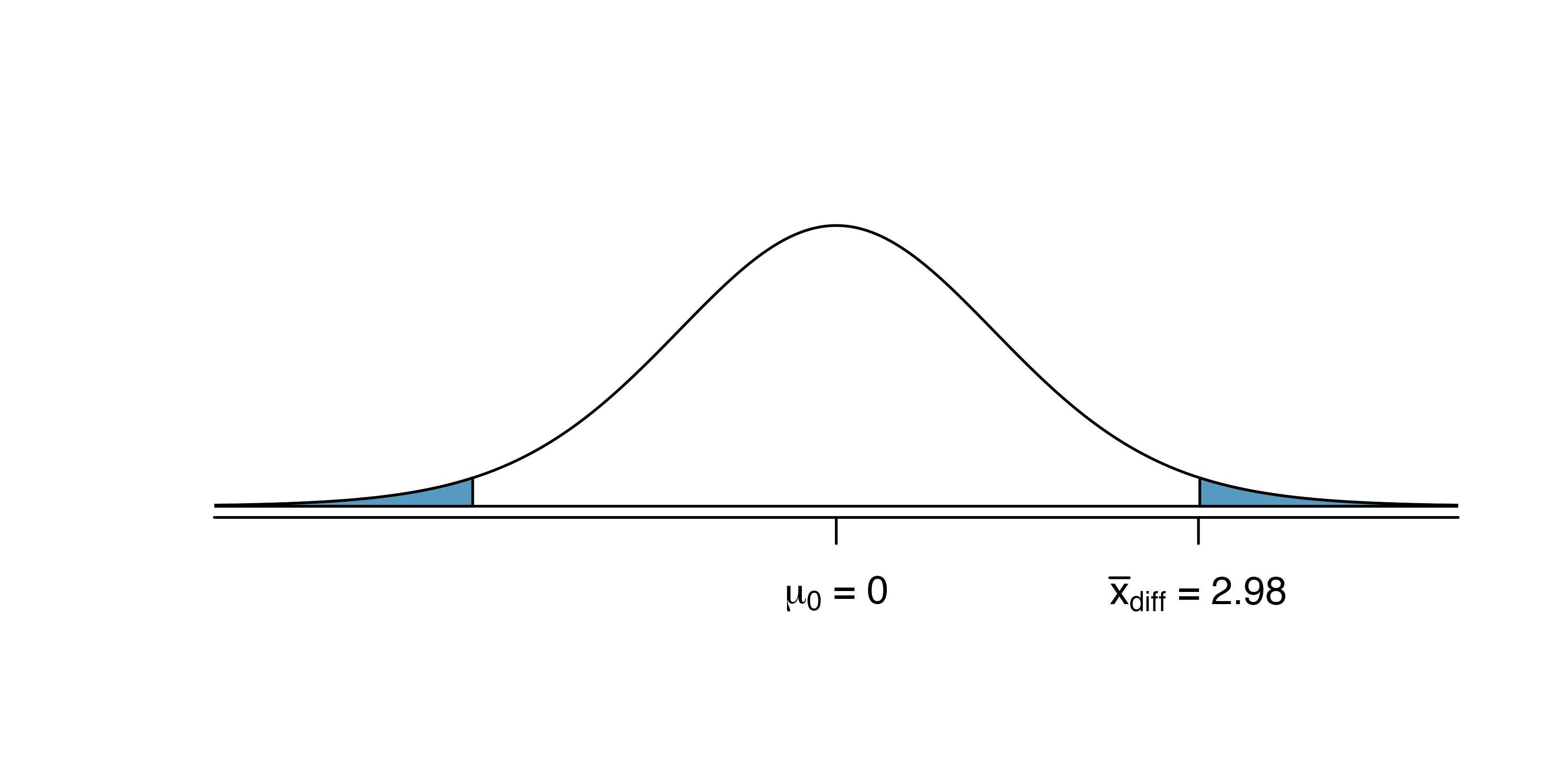
Source: IMS

CI using a normal approximation

Source: IMS

Normal approximation

The normal distribution describes the variability of the different statistics

  • \(\hat{p}\), \(\bar{x}\), \(\hat{\beta}\)

  • simply look at all the histograms we have constructed from simulated samples (HT) and bootstrap samples (CI)!

Classical approach: instead of simulating the sampling distribution via simulation (HT) or bootstrapping (CI), we approximate it with a normal distribution.

Normal approximation for \(\bar{x}\)

We have seen that if a numerical variable \(X\) is normally distributed

\[ X\sim N(\mu, \sigma^2) \]

then the sample average is also normally distributed

\[ \bar{x} \sim N\left(\mu, \frac{\sigma^2}{n}\right) \]

Condition for the normality of \(\bar{x}\)

In practice, we cannot assume that the variable \(X\) is exactly normally distributed.

But as long as

  1. the sample is large, or

  2. the variable is approximately normal: unimodal, roughly symmetric and no serious outlier

\(\bar{x}\) is well approximated by a normal distribution

\[ \bar{x} \sim N\left(\mu, \frac{\sigma^2}{n}\right) \]

See the numerous histograms for case 3 (one mean) where the distribution of \(\bar{x}\) always looks pretty normal.

Normal approximation for \(\hat{p}\)

If

  1. the observations are independent – the independence condition

  2. \(p\) is not extreme and \(n\) is not small \((pn\ge 10 \text{ and } (1-p)n\ge 10)\) – the success-failure condition

the distribution of \(\hat{p}\) can be approximated by a normal distribution

\[ \hat{p} \sim N\left(p, \frac{p(1-p)}{n}\right) \]

Success-failure condition for CI

For CI, we verify the success-failure condition using the sample proportion \(\hat{p}\):

\[ \hat{p}n\ge 10 \text{ and } (1-\hat{p})n\ge 10 \]

Conditions are satisfied

p <- 0.4; n <- 100 # conditions are satisfied: p*n>10 and (1-p)*n>10
results <- tibble(p_hat = numeric())
for(i in 1 : 5e3){
  sim     <- purrr::rbernoulli(n, p)
  p_hat   <- mean(sim)
  results <- results %>% add_row(p_hat)
}
ggplot(results) + geom_histogram(aes(p_hat), binwidth = 0.01)

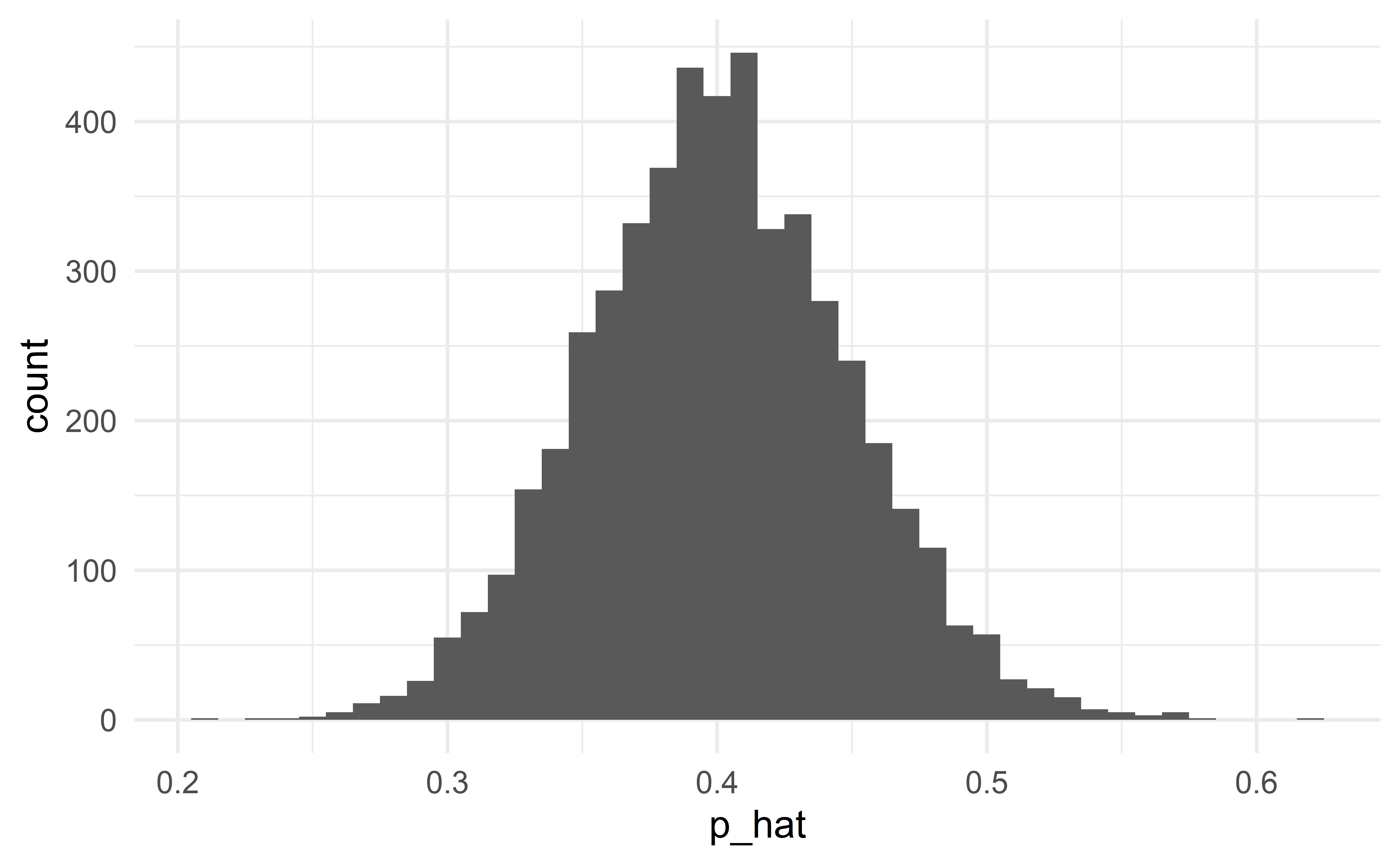
Normal approximation is good

tibble(p_hat = seq(0.2, 0.6, by = 0.001)) %>%
  mutate(normal_approximation = dnorm(p_hat, mean = p, sd = sqrt(p*(1-p)/n))) %>%
  ggplot() +
  geom_line(aes(x = p_hat, y = normal_approximation))

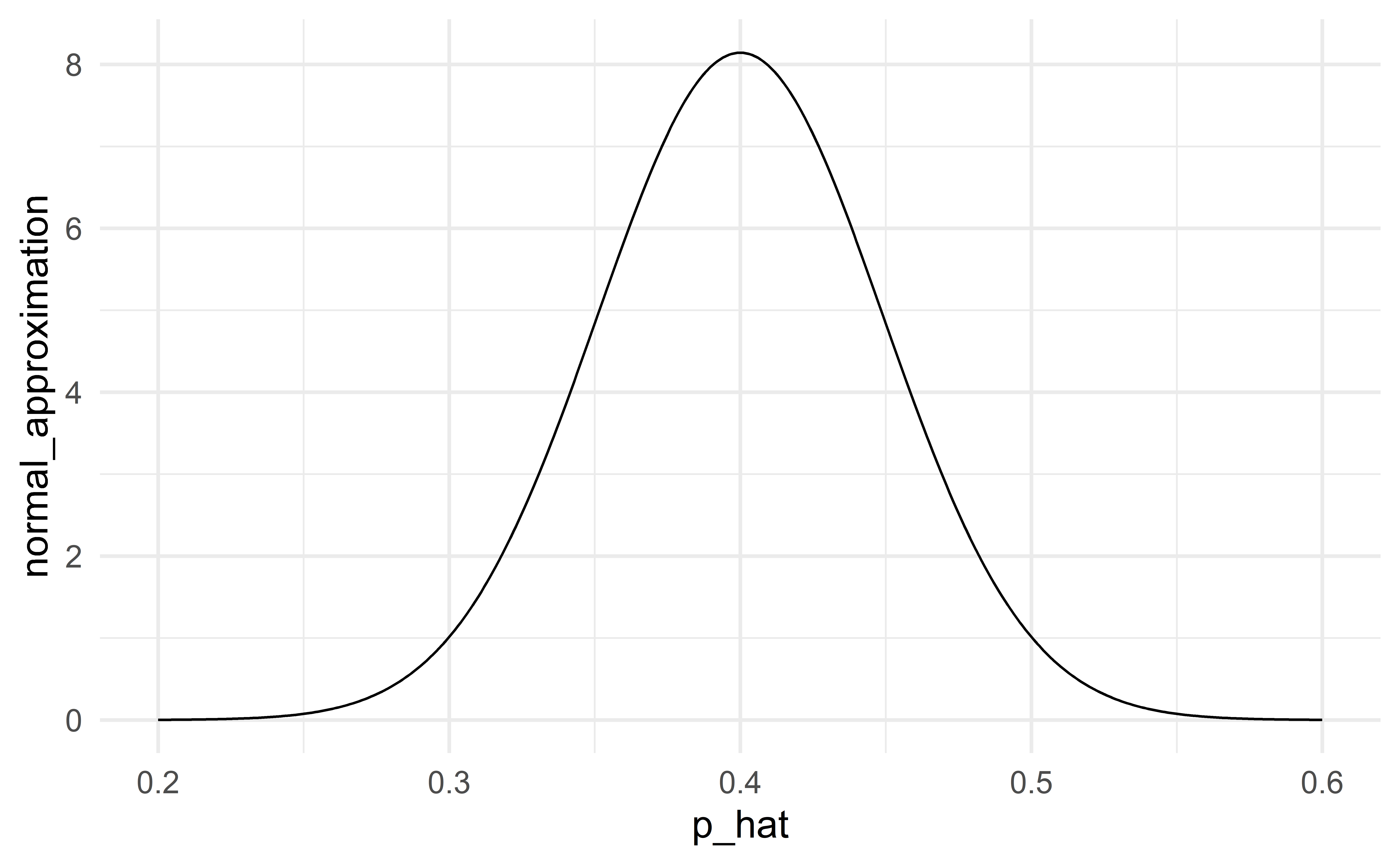
When the conditions are satisfied

When the conditions are satisfied, the normal distribution will be a good approximation. The classical and modern (simulation, bootstrap) approaches to statistical inference will give the same results.

Conditions are not satisfied

p <- 0.025; n <- 100 # conditions are not satisfied: p*n<10 
results <- tibble(p_hat = numeric())
for(i in 1 : 5e3){
  sim     <- purrr::rbernoulli(n, p)
  p_hat   <- mean(sim)
  results <- results %>% add_row(p_hat)
}
ggplot(results) + geom_histogram(aes(p_hat), binwidth = 0.01) + xlim(-0.05, 0.1)

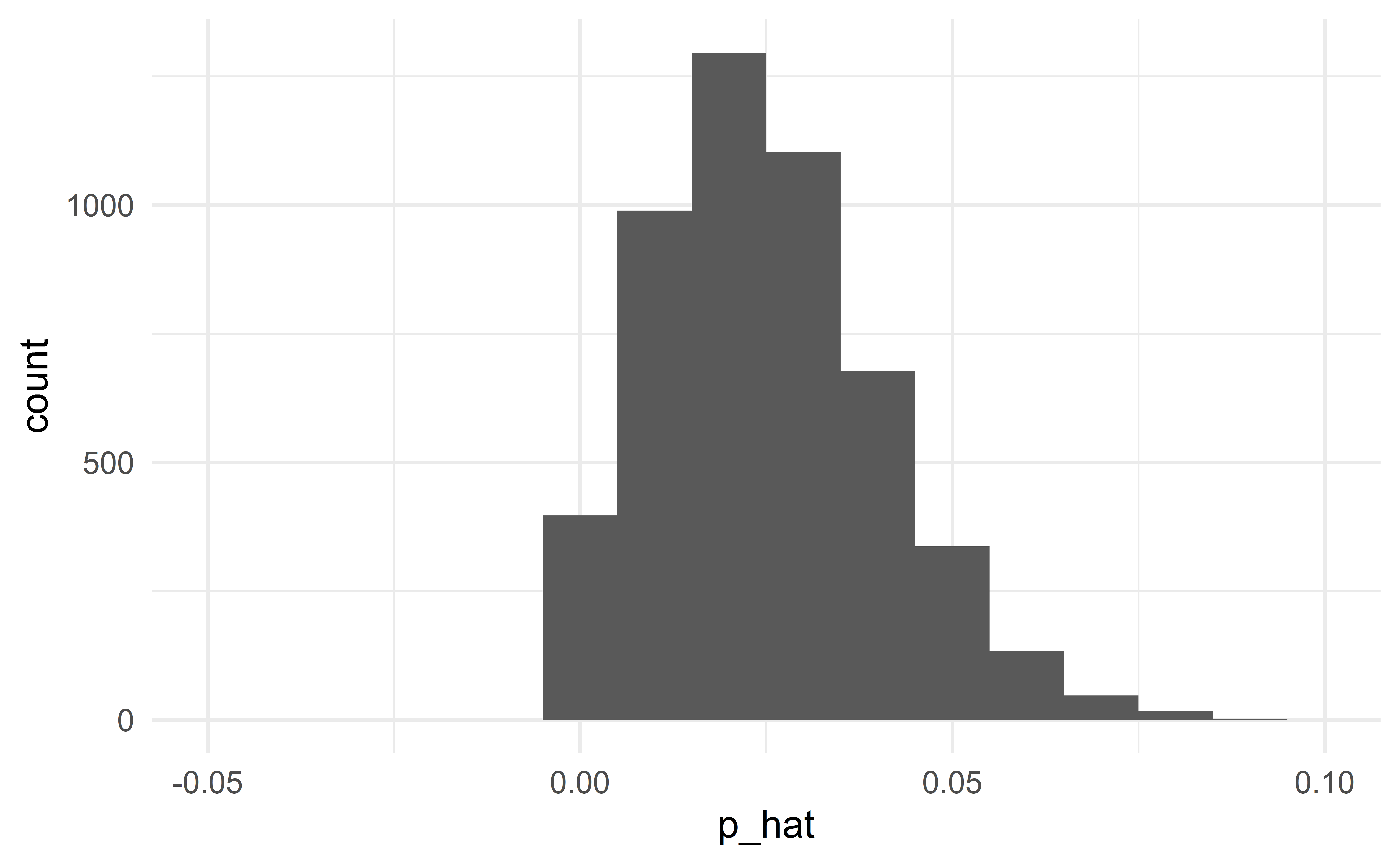
Normal approximation fails

tibble(p_hat = seq(-0.05, 0.1, by = 0.001)) %>%
  mutate(normal_approximation = dnorm(p_hat, mean = p, sd = sqrt(p*(1-p)/n))) %>%
  ggplot() + geom_line(aes(x = p_hat, y = normal_approximation)) + xlim(-0.05, 0.1)

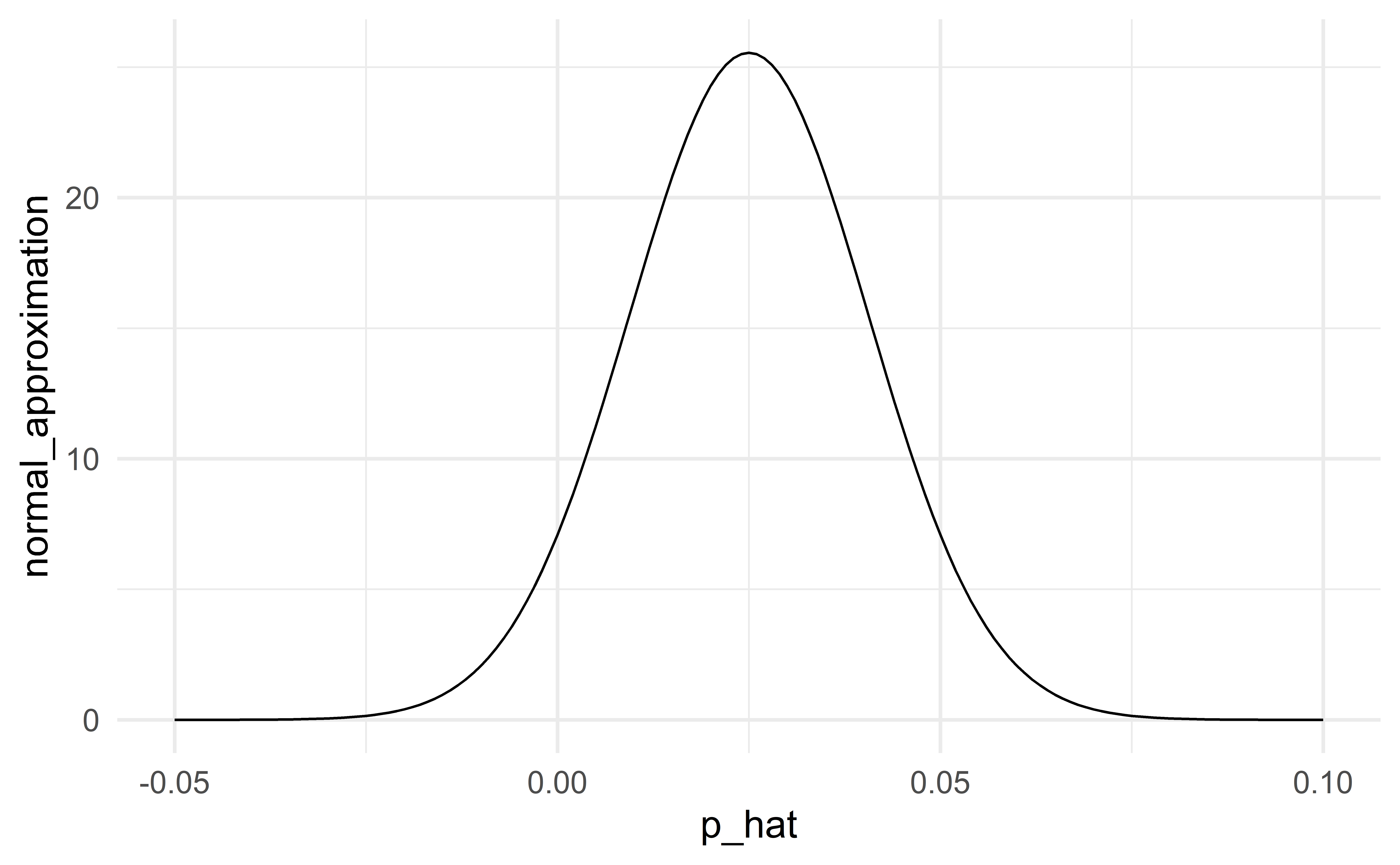
When conditions are not satisfied

When the conditions are not satisfied, the normal distribution will not be a good approximation to the sampling distribution. In this case, we should not use the classical approach to statistical inference, but instead use simulation (HT) or bootstrap (CI).

The classical approach to HT and CI

The classical approach

Step 1: we are interested in the distribution of the statistic under \(H_0\).

  • Modern approach: simulate from this distribution

  • Classical approach: approximate this distribution with a normal distribution

HT

Step 2: we want to compute the p-value

  • Modern approach: the p-value is the proportion of simulations with a statistic at least as extreme as that of the observed sample

  • Classical approach: the p-value is the area under the curve of the normal distribution that is at least as extreme as the observed statistic.

What R does

R will compute the p-value for you. Here is what R does behind the scene:

CI

Step 2: identify the upper and lower bounds of the CI

  • Modern approach: find the appropriate percentiles among the simulated values

  • Classical approach:find the appropriate percentiles of the normal approximation

What R does

R will compute the upper and lower bounds for you. Here is what R does behind the scene:

Case 1 – one proportion

n <- 1500 # sample size
x <- 780  # number of successes
prop.test(
  x, n,             # observed data
  p = 0.5,          # value in the null hypothesis
  conf.level = 0.99 # confidence level for CI
  )

    1-sample proportions test with continuity correction

data:  x out of n, null probability 0.5
X-squared = 2.3207, df = 1, p-value = 0.1277
alternative hypothesis: true p is not equal to 0.5
99 percent confidence interval:
 0.4864251 0.5533970
sample estimates:
   p 
0.52

Comparison with simulation-based HT

The simulation-based HT yielded a p-value of 0.127.

A good normal approximation

When the conditions for the normal approximation are satisfied, the results based on simulations (modern) and the normal approximation (classical) will be similar.

Conditions: independence, success-failure condition

Individual exercise - the classical approach for one proportion

Suppose you interview 2000 US adults about their political preferences and 1200 of them say that they are democrat. What is the 95% confidence interval for \(p\), the proportion of US adults who are democrats? What is the length of the interval?

What 95% CI do you obtain if 6000 out of 10000 US adults say they are democrat? What is its length?

Exercise 16.19 – find the 95% CI. Are the conditions satisfied?

Exercise 16.21

Exercise 16.25

05:00

Case 2 – two proportions

Consider the gender discrimination study.

n_m <- 24; n_f <- 24 # sample sizes
x_m <- 14; x_f <- 21 # numbers of promotions
prop.test(c(x_m, x_f), c(n_m, n_f))

    2-sample test for equality of proportions with continuity correction

data:  c(x_m, x_f) out of c(n_m, n_f)
X-squared = 3.7978, df = 1, p-value = 0.05132
alternative hypothesis: two.sided
95 percent confidence interval:
 -0.57084188 -0.01249145
sample estimates:
   prop 1    prop 2 
0.5833333 0.8750000

Conditions

  1. Independence within groups (same as case 1)

  2. Independence between groups

  3. Success-failure condition for each group (10 successes and 10 failures in each group)

Comparison with simulation-based HT

Using the simulation-based HT, we found a p-value of 0.0435.

A good normal approximation

When the conditions for the normal approximation are not satisfied, the results based on simulations (modern) and the normal approximation (classical) may differ.

A simulation-based HT will always give exact results. A HT based on the normal distribution will only give the same (exact) results when the conditions are satisfied.

Individual exercise - the classical approach for two proportions

Exercise 17.7

Exercise 17.13

Exercise 17.19

06:00

Case 3 – one mean

d <- ggplot2::mpg
t.test(d$hwy, mu = 25)

    One Sample t-test

data:  d$hwy
t = -4.0071, df = 233, p-value = 0.00008274
alternative hypothesis: true mean is not equal to 25
95 percent confidence interval:
 22.67324 24.20710
sample estimates:
mean of x 
 23.44017

Conditions

  1. Independence

  2. Normality – can be relaxed for larger samples \((n\ge30)\)

Statistics as an art

The normality assumption is vague. The most important feature of the sample to verify is the presence of outliers.

Rule of thumb: if \(n<30\), there should not be any clear outlier; if \(n\ge30\), there should not be any extreme outlier.

Individual exercise - the classical approach for one mean

Make a histogram and a boxplot of the variable. Are the conditions satisfied?

Construct a 99% CI for hwy.

Hint: run the command help(t.test) to access the help file of the function t.test and see what parameter determines the confidence level.

03:00

Case 4 – two means

There are two implementation; which one is more convenient depends on the structure of the data.

d <- ggplot2::mpg
t.test(hwy ~ year, data = d)

    Welch Two Sample t-test

data:  hwy by year
t = -0.032864, df = 231.64, p-value = 0.9738
alternative hypothesis: true difference in means between group 1999 and group 2008 is not equal to 0
95 percent confidence interval:
 -1.562854  1.511572
sample estimates:
mean in group 1999 mean in group 2008 
          23.42735           23.45299 
d <- ggplot2::mpg
t.test(d$cty, d$hwy)

    Welch Two Sample t-test

data:  d$cty and d$hwy
t = -13.755, df = 421.79, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -7.521683 -5.640710
sample estimates:
mean of x mean of y 
 16.85897  23.44017

Conditions

  1. Independence within groups

  2. Independence between groups

  3. Normality in each group (same as case 3 – one mean)

Individual exercise - the classical approach for two means

What is the 99% CI for the difference in fuel efficiency on the highway and in the city? What is the length of this CI?

Are the conditions satisfied?

01:00

Case 4bis – paired means

d <- ggplot2::mpg
t.test(d$cty, d$hwy, paired = TRUE)

    Paired t-test

data:  d$cty and d$hwy
t = -44.492, df = 233, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.872628 -6.289765
sample estimates:
mean of the differences 
              -6.581197

Conditions

  1. Paired observations

  2. Independence between pairs

  3. Normality

Individual exercise - the classical approach for paired means

What is the 99% CI for the difference in fuel efficiency on the highway and in the city? What is the length of this CI? Compare it with the CI obtained when the observations were not paired.

01:00

Always pair the observations

If the data can paired, you should always do it! Pairing data yields an analysis that is more powerful:

  • narrower CI

  • smaller p-value

Case 5 – regression

m <- lm(hwy ~ cty, data = mpg)
tidy(m)
# A tibble: 2 x 5
  term        estimate std.error statistic   p.value
  <chr>          <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept)    0.892    0.469       1.90 5.84e-  2
2 cty            1.34     0.0270     49.6  1.87e-125
m <- lm(hwy ~ cty + displ, data = mpg)
tidy(m)
# A tibble: 3 x 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)   1.15      1.21       0.949 3.43e- 1
2 cty           1.33      0.0449    29.6   1.43e-80
3 displ        -0.0343    0.148     -0.232 8.17e- 1
d <- heart_transplant %>% mutate(survived_binary = survived == "alive")
m <- glm(survived_binary ~ age + transplant, family = "binomial", data = d)
tidy(m)
# A tibble: 3 x 5
  term                estimate std.error statistic p.value
  <chr>                  <dbl>     <dbl>     <dbl>   <dbl>
1 (Intercept)           0.973     1.08       0.904 0.366  
2 age                  -0.0763    0.0255    -2.99  0.00277
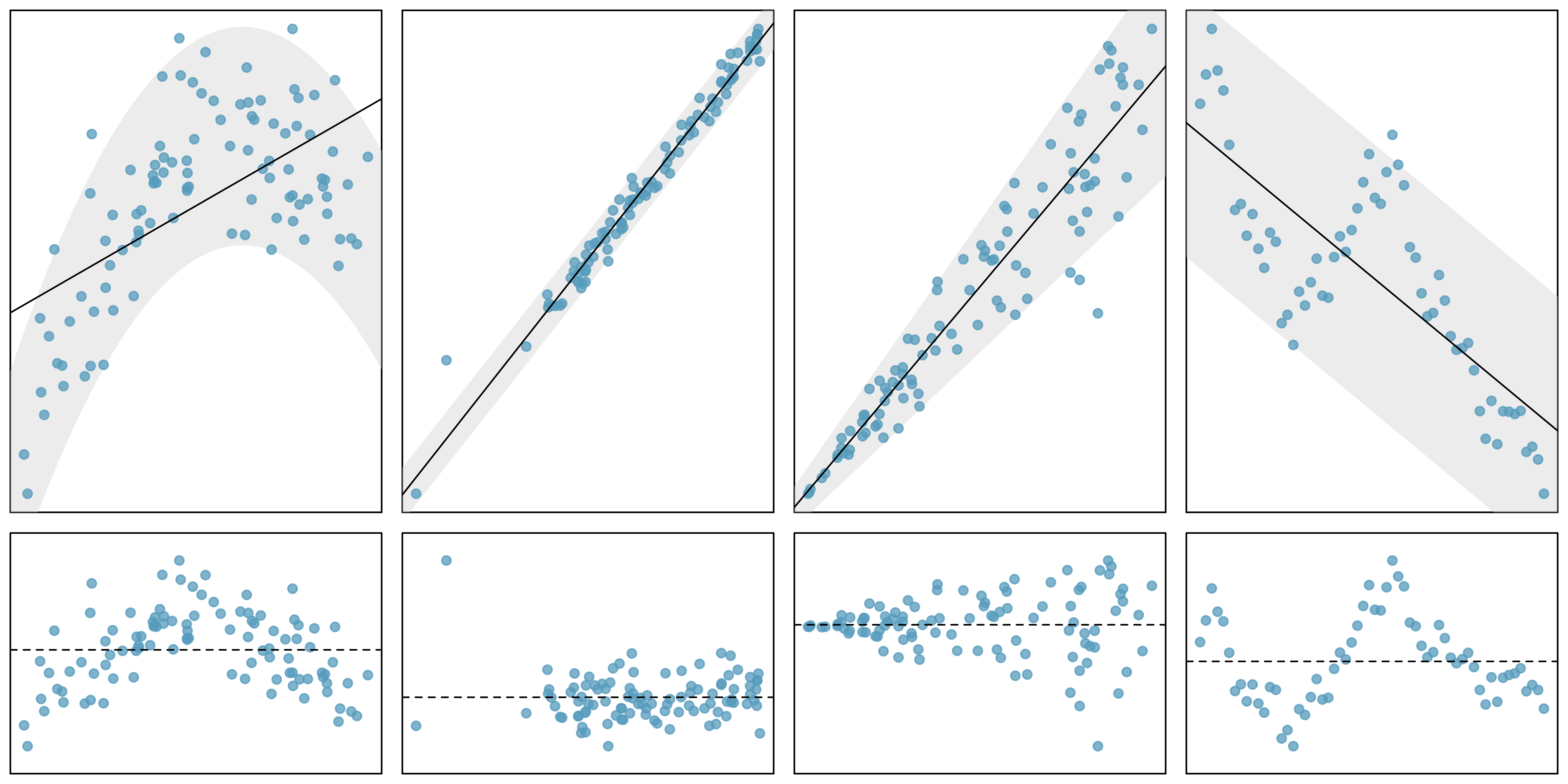
3 transplanttreatment   1.82      0.668      2.73  0.00635

Conditions (LINE) – linear regression

  1. Linearity

  2. Independence

  3. Normality

  4. Equal variability (homoskedasticity)

\(\Rightarrow\) verify with a residual plot!

Data sets

Individual exercise - the classical approach for regression

What condition(s) are violated by each of the following data sets (see next slide)?

Exercise 24.10

Exercise 24.13 – parts a and b

Exercise 24.15 – part b

Exercise 25.3

Exercise 25.7

Exercise 26.1

05:00

Standard error

Standard error

Standard error (SE): standard deviation of the normal approximation.

The SE measures the variability of the statistic.

  • \(SE(\hat{p})=\sqrt{\frac{p(1-p)}{n}}\)

  • \(SE(\hat{p}_{diff})=\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}\)

  • \(SE(\bar{x}) = \sqrt{\frac{\sigma^2}{n}}\)

  • \(SE(\bar{x}_{diff}) = \sqrt{\frac{\sigma^2_1}{n_1}+\frac{\sigma^2_2}{n_2}}\)

  • \(SE(\hat{\beta})\) has a complicated form.

Sample size and SE

Note the role of the sample size on the SE!

Larger samples have a smaller SE

Sample size matters

Larger \(n\)

\(\Rightarrow\) smaller SE

\(\Rightarrow\) normal approximation with smaller sd

\(\Rightarrow\) normal approximation is more concentrated

\(\Rightarrow\) tighter CI and smaller p-value.

Individual exercise - sample size and CI

Exercise 16.13 – part e

Exercise 16.15 – part b

Exercise 13.4 – part d

02:00

Case 6 – many proportions (\(\chi^2\) test)

Reproducibility

ask <- openintro::ask %>%
  mutate(
    response = if_else(response == "disclose", "Disclose problem", "Hide problem"),
    question_class = case_when(
      question_class == "general" ~ "General",
      question_class == "neg_assumption" ~ "Negative assumption",
      question_class == "pos_assumption" ~ "Positive assumption"
    ),
    question_class = fct_relevel(question_class, "General", "Positive assumption", "Negative assumption")
  )

Example – defective iPod

Question Disclose problem Hide problem Total
General 2 71 73
Positive assumption 23 50 73
Negative assumption 36 37 73
Total 61 158 219

Source: IMS

HT, no CI

\(H_0\): the response is independent of the question asked

\(H_a\): the response depends on the question asked

We will not quantify the differences between the three question with CIs.

Expected counts

Disclose problem
Hide problem
Total
General 2 (20.33) 71 (52.67) 73
Positive assumption 23 (20.33) 50 (52.67) 73
Negative assumption 36 (20.33) 37 (52.67) 73
Total 61 NA 158 NA 219

Source: IMS

Chance or effect?

Is the difference between the expected and observed counts is due to

  • chance alone, or

  • the fact that the way people responded depended on the question asked?

\(\chi^2\) (“Kai-squared”) statistic:

\[ \chi^2 = \dfrac{(O_{11} - E_{11})^2}{E_{11}} + \dfrac{(O_{21} - E_{21})^2}{E_{21}} + \dots + \dfrac{(O_{32} - E_{32})^2}{E_{32}} \]

Computing \(\chi^2\)

\[ \begin{aligned} &\text{General formula} && \frac{(\text{observed count } - \text{expected count})^2} {\text{expected count}} \\ &\text{Row 1, Col 1} && \frac{(2 - 20.33)^2}{20.33} = 16.53 \\ &\text{Row 2, Col 1} && \frac{(23 - 20.33)^2}{20.33} = 0.35 \\ & \hspace{9mm}\vdots && \hspace{13mm}\vdots \\ &\text{Row 3, Col 2} && \frac{(37 - 52.67)^2}{52.67} = 4.66 \end{aligned} \]

\[\chi^2 = 16.53 + 0.35 + \dots + 4.66 = 40.13\]

Source: IMS

The approximate distribution of \(\chi^2\)

When the conditions of

  1. independence

  2. \(>5\) expected counts per cell

are satisfied, the \(\chi^2\) statistic approximately follows a \(\chi^2\) distribution.

Computing the p-value

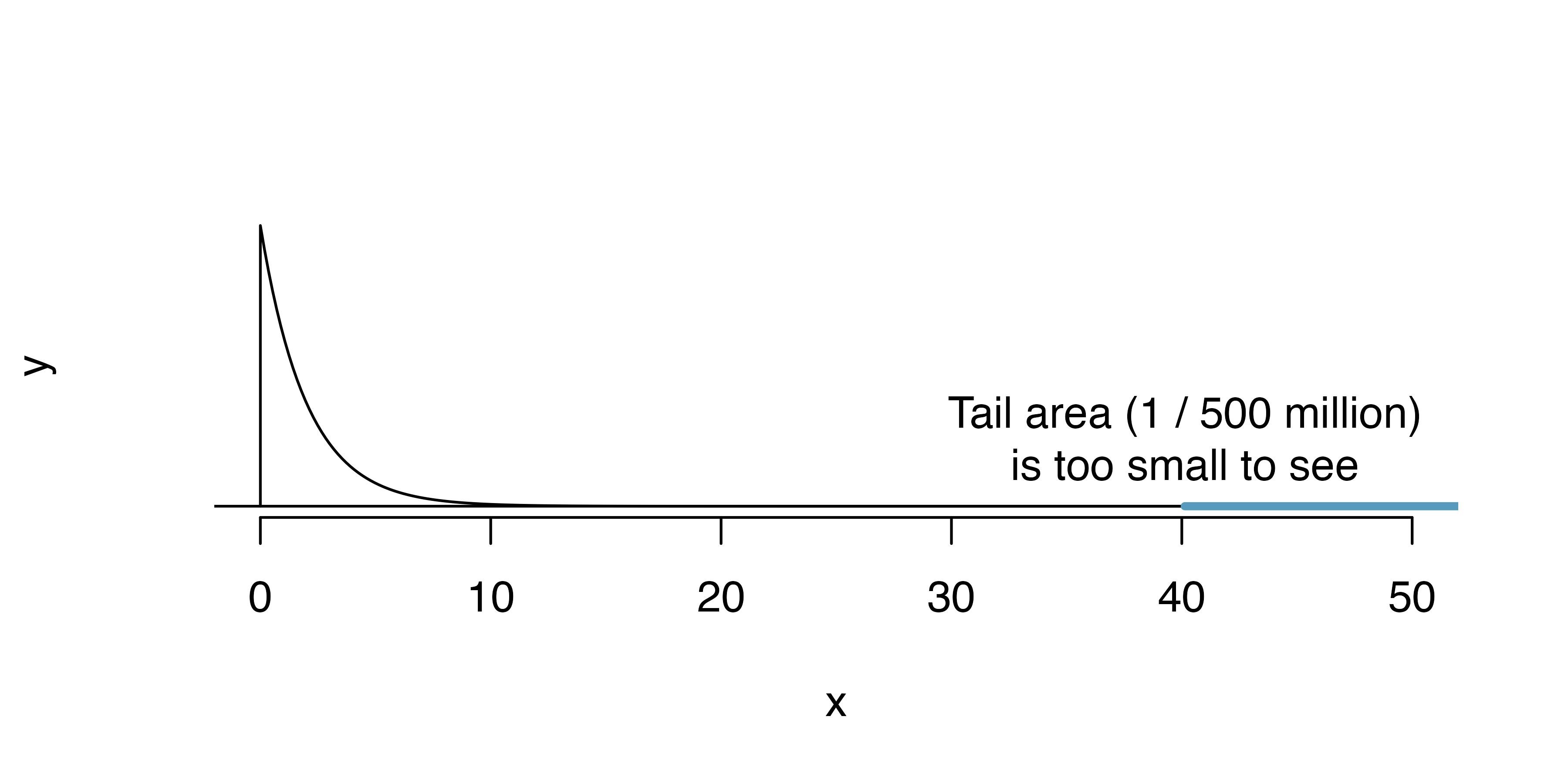
Source: IMS

The \(\chi^2\) test in R

head(ask)
# A tibble: 6 x 3
  question_class      question                               response        
  <fct>               <chr>                                  <chr>           
1 General             What can you tell me about it?         Hide problem    
2 Positive assumption It doesn't have any problems, does it? Hide problem    
3 Positive assumption It doesn't have any problems, does it? Disclose problem
4 Negative assumption What problems does it have?            Disclose problem
5 General             What can you tell me about it?         Hide problem    
6 Negative assumption What problems does it have?            Disclose problem
chisq.test(ask$response, ask$question_class)

    Pearson's Chi-squared test

data:  ask$response and ask$question_class
X-squared = 40.128, df = 2, p-value = 0.000000001933

Individual exercise - \(\chi^2\) test

Exercise 18.15

01:30

HT via simulation

When the conditions are not met, you need to conduct a HT via simulation.

  1. Simulate artificial samples under \(H_0\) by shuffling the response variable
  2. Compute the \(\chi^2\) statistic of each simulated sample
  3. Determine how extreme the \(\chi^2\) statistic of the observed sample is by computing a p-value

See Section 18.1 for an example.

Case 7 – many means (ANOVA)

Reproducibility

mlb_players_18 <- openintro::mlb_players_18 %>%
  filter(
    AB >= 100, 
    !position %in% c("P", "DH")
  ) %>%
  mutate(
    position = case_when(
      position %in% c("LF", "CF", "RF")       ~ "OF",
      position %in% c("1B", "2B", "3B", "SS") ~ "IF",
      TRUE                                    ~ position
    ),
    position = fct_relevel(position, "OF", "IF", "C")
  )

Example – batting performance and position

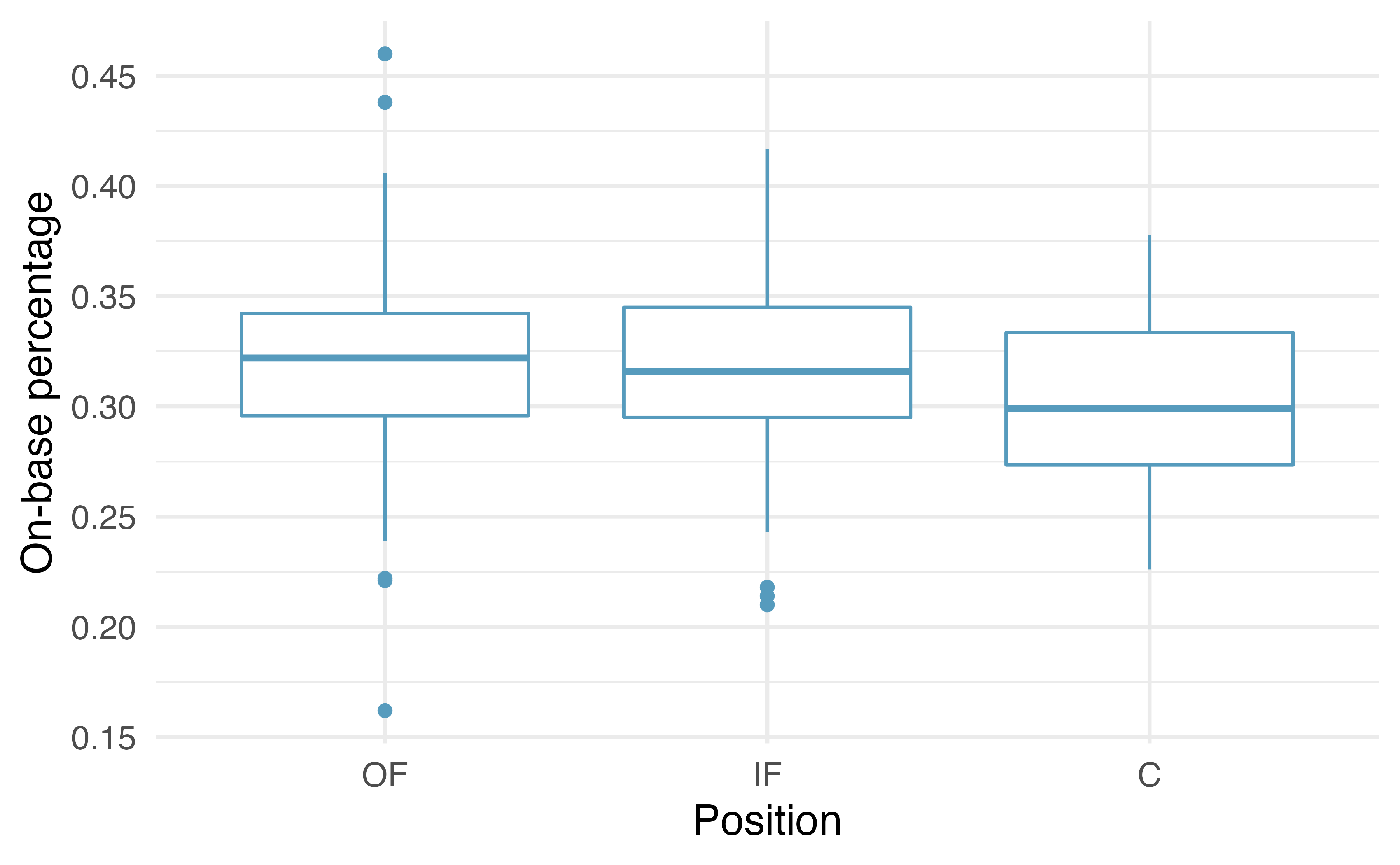
Source: IMS

HT, no CI

\(H_0: \mu_{OF} = \mu_{IF} = \mu_{C}\): (the batting performance is the same across all three positions)

\(H_a\): at least one mean is different

We will not quantify the differences between the three positions with CIs.

ANOVA in R

m <- aov(OBP ~ position, data = mlb_players_18)
tidy(m)
# A tibble: 2 x 6
  term         df  sumsq  meansq statistic  p.value
  <chr>     <dbl>  <dbl>   <dbl>     <dbl>    <dbl>
1 position      2 0.0161 0.00803      5.08  0.00662
2 Residuals   426 0.674  0.00158     NA    NA

Conditions

  1. Independence within

  2. Independence between

  3. Normality (sample size and outliers)

  4. Constant variance

Verify assumptions 3 and 4 with side-sby-side histograms

Side-by-side histograms

ggplot(mlb_players_18) +
  geom_histogram(aes(OBP)) +
  facet_grid(position ~ .)

Individual exercise - ANOVA

Exercise 22.5

Exercise 22.9 – parts a and b

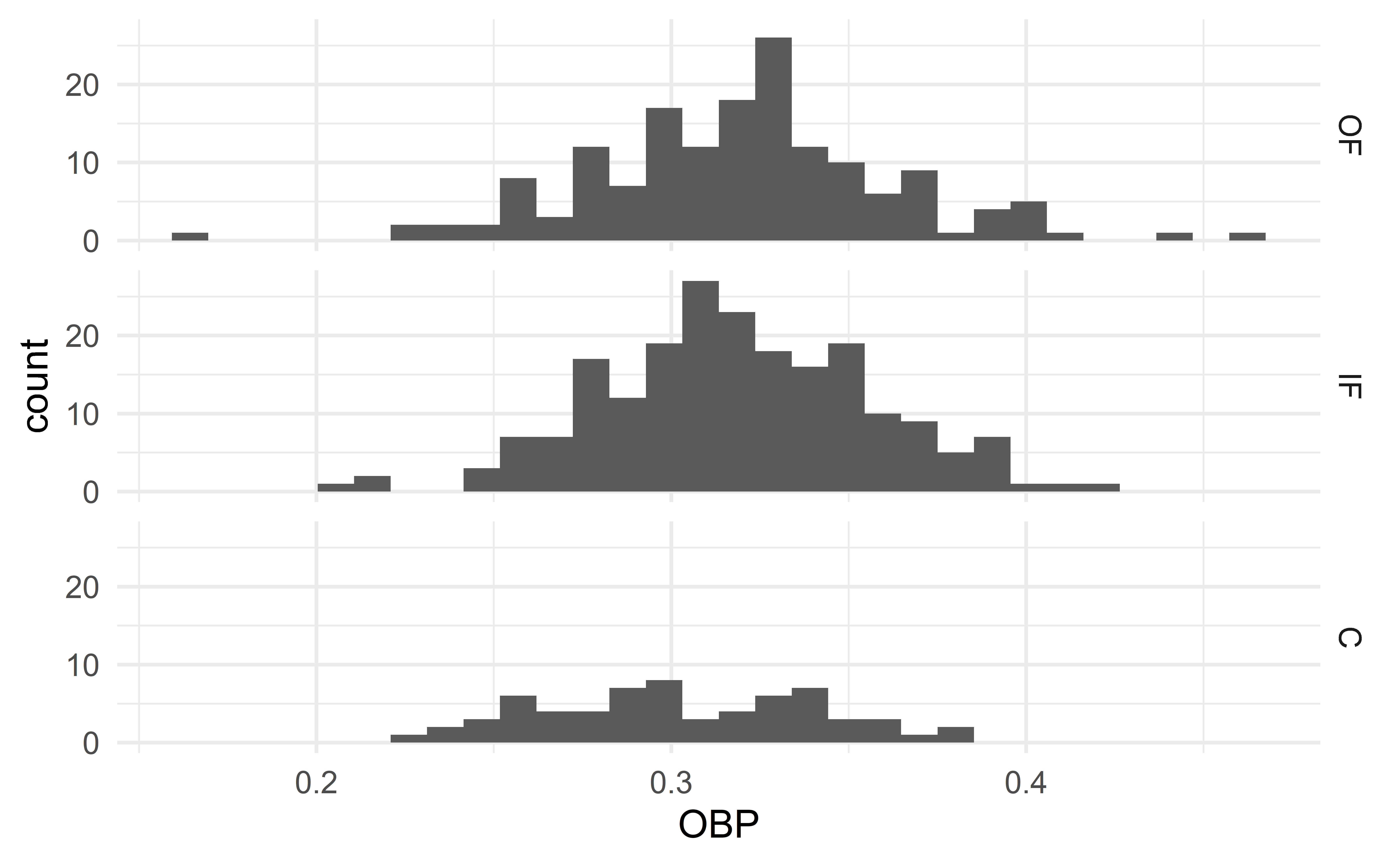
03:00

HT via simulation

When the conditions are not met, you need to conduct a HT via simulation.

  1. Simulate artificial samples under \(H_0\) by shuffling the response variable
  2. Compute the \(F\) statistic of each simulated sample (see Section 22.2)
  3. Determine how extreme the \(F\) statistic of the observed sample is by computing a p-value

See Section 22.2 for an example.

Recap

Recap

  • Normal approximation
  • Classical approach to statistical inference
  • Standard error
  • Case 6 – many proportions (\(\chi^2\) test)
  • Case 7 – many means (ANOVA)

https://rmorsomme.github.io/website/