Inference for means

STA 101L - Summer I 2022

Raphael Morsomme

Welcome

Announcements

  • Homework 6 due Thursday

  • Inference project

    • Start to think about data or a question that interests you.

  • Remaining homework due on Mon/Thu instead of Wed/Sun?

Announcements

Midterm survey

  • review holdout and CV

  • more live coding (?)

  • more individual assignments in class

  • OH before Sunday’s HW \(\Rightarrow\) HW due on Monday (OH Monday morning)

  • website

    • external links will open a new window

    • slide changes will not be pushed to browser history

  • see these steps to print the slides

Recap

  • One proportion

    • HT via simulation

    • CI via bootstrap

  • Two proportions

    • HT via simulation

    • CI via bootstrap

Outline

  • The normal distribution
  • One mean (case 3)
  • Two means (case 4)
  • Paired means (case 3)

The normal distribution

The normal distribution

The distribution of a numerical variable is often modeled with a normal distribution.

tibble(x = seq(-5, 5, by = 0.01)) %>%
  mutate(normal = dnorm(x, mean = 0, sd = 1)) %>%
  ggplot() + 
  geom_line(aes(x, normal))

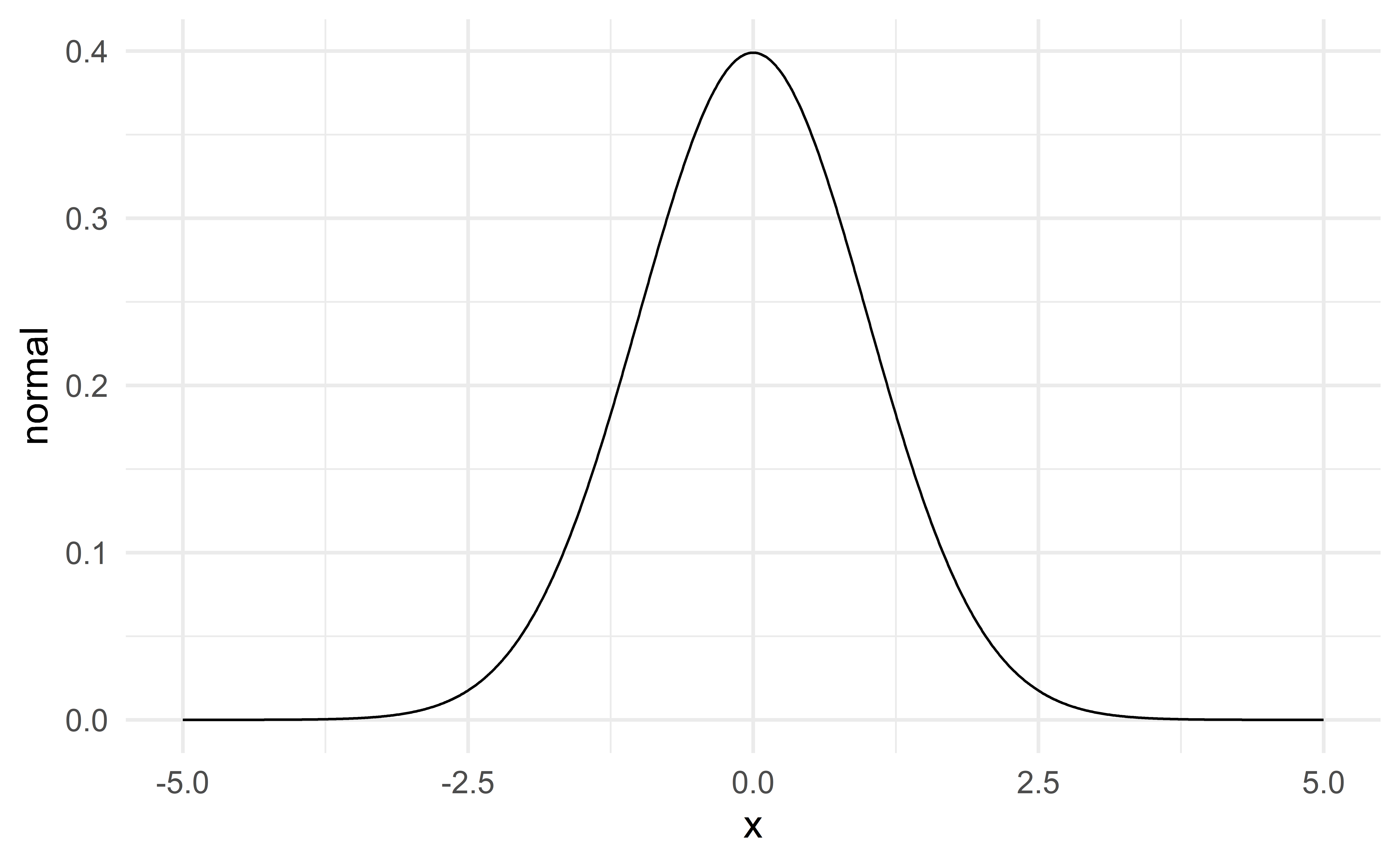
Two parameters

The mean (\(\mu\)) – location

The standard deviation (\(\sigma\)) – spread

\[ N(\mu, \sigma) \] The standard normal distribution \(N(\mu = 0, \sigma = 1)\) is plotted on the previous slide.

Individual exercise - normal distribution

Modify the following R code to plot the two normal distributions

  • \(N(\mu = 0, \sigma = 0.5)\)
  • \(N(\mu = 1, \sigma = 0.5)\)
tibble(x = seq(-5, 5, by = 0.01)) %>%
  mutate(normal = dnorm(x, mean = 0, sd = 1)) %>%
  ggplot() + 
  geom_line(aes(x, normal))
03:00

Property I

If the variable \(X\sim N(\mu, \sigma)\), then for any number \(a\) and \(b\)

\[ X + a \sim N(\mu+a, \sigma), \]

\[ bX \sim N(b\mu, b \sigma) \]

and

\[ bX + a \sim N(b\mu+a, b\sigma). \]

Property II

If the variables \(X\sim N(\mu_1, \sigma_1)\) and \(Y\sim N(\mu_2, \sigma_2)\) are independent, then

\[ X+Y \sim N(\mu_{tot} = \mu_1 + \mu_2, \sigma_{tot} = \sqrt{\sigma_1^2 + \sigma_2^2}) \]

Alternative parameterization

\(N(\mu, \sigma^2)\), where \(\sigma^2\) is the variance.

Property I gives

\[ bX + a \sim N(b\mu + a, b^2 \sigma^2) \]

and property II gives

\[ X+Y \sim N(\mu_{tot} = \mu_1 + \mu_2, \sigma_{tot}^2 = \sigma_1^2 + \sigma_2^2) \]

The mean of the sum is the sum of the means.

The variance of the sum is the sum of the variances.

Individual exercise - normal property

Suppose you have a sample with \(n=10\) independent observations in which each observation follows a standard normal distribution. That is,

\[ X_1 \sim N(0,1), X_2 \sim N(0,1), \dots, X_{10} \sim N(0, 1). \]

Use the normal properties to derive the distribution of the sample average

\[ \bar{x} = \dfrac{X_1 + X_2 + \dots + X_{10}}{10} \]

What happens to the sd/variance of \(\bar{x}\) as the sample size \(n\) increases?

04:00

Individual exercise -

Exercise 19.5 – for our purpose in part b standard error is equivalent to standard deviation.

02:00

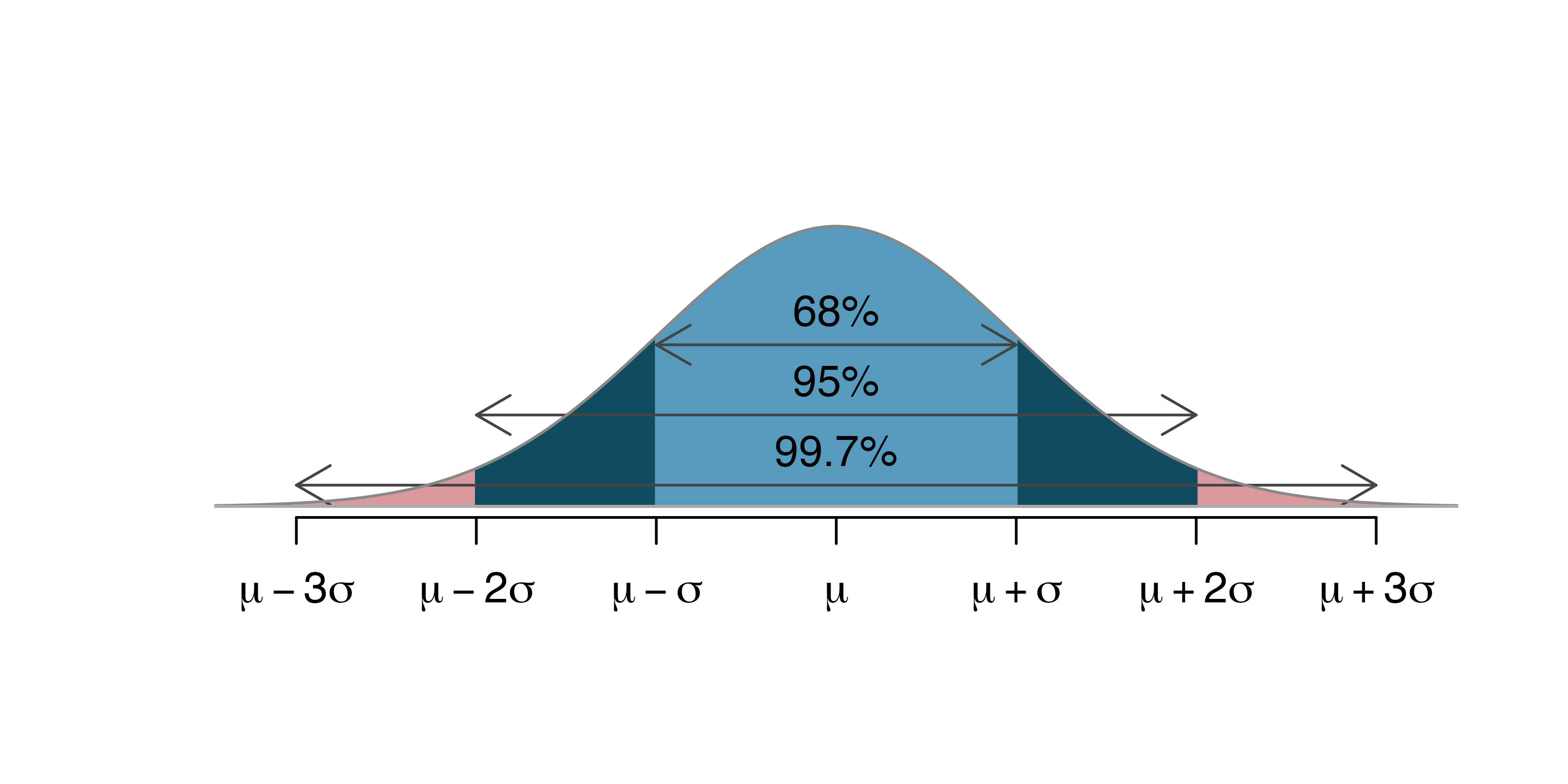
The 68, 95, 99.7 rule

One mean

Setup

Population parameter: mean \(\mu\)

Sample statistic: sample average \(\bar{x}\)

Hypothesis testing:

  • \(H_0:\mu=\mu_0\) where \(\mu_0\) is a fixed number

  • \(H_a:\mu\neq \mu_0\)

Confidence interval: range of plausible values for \(\mu\).

Individual exercise - statistic and parameter

Exercise 19.1

01:00

Example – car price

What is the average price of a car on Awesome Car?

\[\begin{align*} \bar{x} & = \dfrac{18,300+20,100+9,600+10,700+27,000}{5} \\ & = 17,140 \end{align*}\]

Source: IMS

Hypothesis test via simulation

Normal model

Let us assume that car prices follow a normal distribution with mean \(\mu\) and sd \(\sigma\):

\[ \text{price} \sim N(\mu, \sigma) \]

\(H_0:\mu=10,000\)

\(H_a:\mu\neq 10,000\)

  • Simulate many samples under \(H_0\).

  • Determine if the observed data could have plausibly arisen under \(H_0\).

Problem

To simulate from the normal distribution, we need to specify both the mean \(\mu\) and the sd \(\sigma\).

Problem: under \(H_0\) we only know that \(\mu = 10,000\); we do not know what value to use for \(\sigma\)!

\(\Rightarrow\) We cannot conduct a hypothesis test via simulation!

Confidence interval via bootstrap

Bootstrapping

Sample with repetition from the observed sample to construct many bootstrap samples.

Bootstrap samples \(\Rightarrow\) sampling distribution \(\Rightarrow\) CI

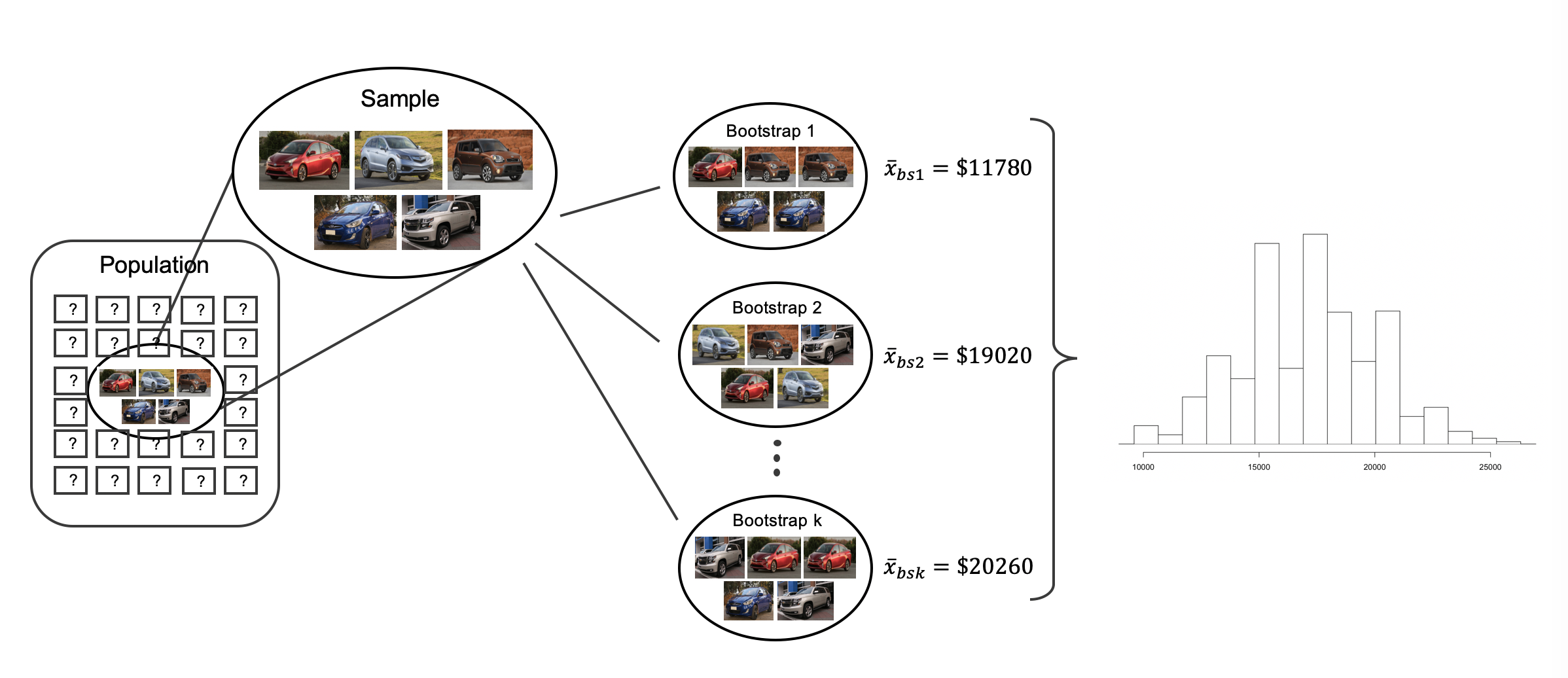
Source: IMS

Bootstrap in R

sample_observed <- tibble(price = c(18300, 20100, 9600, 10700, 27000))
sample_bootstrap <- function(data){ # same function as before
  n                <- nrow(data)
  sample_bootstrap <- slice_sample(data, n = n, replace = TRUE)
  return(sample_bootstrap)
}
set.seed(1)
sample_bootstrap(sample_observed)
# A tibble: 5 x 1
  price
  <dbl>
1 18300
2 10700
3 18300
4 20100
5 27000

results <- tibble(stat_boot = numeric())
set.seed(0)
for(i in 1 : 1e3){
  d_boot    <- sample_bootstrap(sample_observed) # bootstrap sample
  stat_boot <- mean(d_boot$price)                # bootstrap statistic
  results   <- results %>% add_row(stat_boot) 
}
quantile(results$stat_boot, c(0.025, 0.975)) # 95% CI
 2.5% 97.5% 
11780 23520 
quantile(results$stat_boot, c(0.01 , 0.99 )) # 98% CI (wider)
     1%     99% 
11557.8 24240.0 

ggplot(results) + 
  geom_histogram(aes(stat_boot), binwidth = 1350) + 
  geom_vline(xintercept = quantile(results$stat_boot, c(0.025, 0.975)), col = "gold1", size = 2) + # 95% CI 
  geom_vline(xintercept = quantile(results$stat_boot, c(0.01 , 0.99)), col = "maroon", size = 2) # 98% CI

Group exercise - Bootstrap CI

Exercises 19.11 and 19.13

03:00

CI for the standard deviation \(\sigma\)

results <- tibble(stat_boot = numeric())
set.seed(0)
for(i in 1 : 1e3){
  d_boot    <- sample_bootstrap(sample_observed)
  stat_boot <- sd(d_boot$price  )              # sd instead of mean
  results   <- results %>% add_row(stat_boot) 
}

ggplot(results) + 
  geom_histogram(aes(stat_boot)) + 
  geom_vline(xintercept = quantile(results$stat_boot, c(0.05 , 0.95 )), col = "gold1", size = 2) + # 90% CI 
  geom_vline(xintercept = quantile(results$stat_boot, c(0.01, 0.99)), col = "maroon", size = 2) # 98% CI

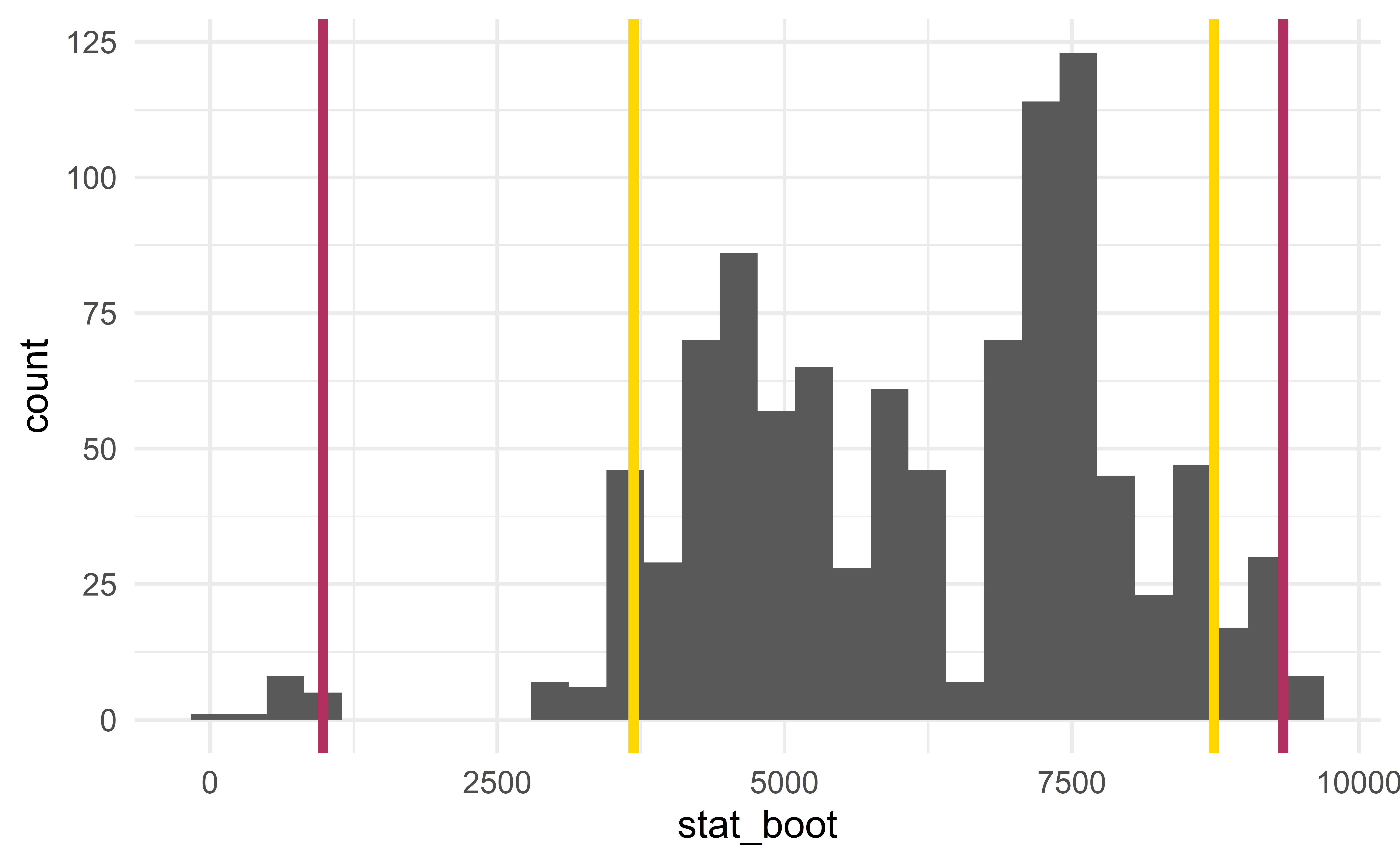
Any statistic, but not any sample

Bootstrap any statistic

You can bootstrap almost any statistic you want!

The quality of the sample matters!

A statistical analysis can only be as good as the sample collected. Here, a sample of \(5\) cars contains very limited information about the population; it would be useful to have a larger sample.

Two means

Setup

A population divided in two groups.

Population parameter: difference in mean

\[ \mu_{diff}=\mu_1-\mu_2 \]

Sample statistic: difference in proportion in the sample

\[ \bar{x}_{diff}=\bar{x}_1-\bar{x}_2 \]

\(H_0:\mu_{diff}=0\) (no difference between the two groups)

\(H_a:\mu_{diff}\neq0\)

Individual exercise -

Exercise 20.1

01:30

Example – two class exams

A professor considers two designs for an exam. Are the two types of exam equally difficult?

d <- openintro::classdata %>% 
  filter(lecture %in% c("a", "b")) %>%
  rename(score = m1, exam = lecture)
d
# A tibble: 113 x 2
   score exam 
   <dbl> <fct>
 1    67 a    
 2    59 a    
 3   100 a    
 4    81 a    
 5    80 a    
 6    63 a    
 7   100 a    
 8    44 a    
 9    82 a    
10    67 a    
# ... with 103 more rows

ggplot(d, aes(score, exam, col = exam)) + 
  geom_boxplot() +
  geom_jitter(width = 0, height = 0.1) # add vertical jitter

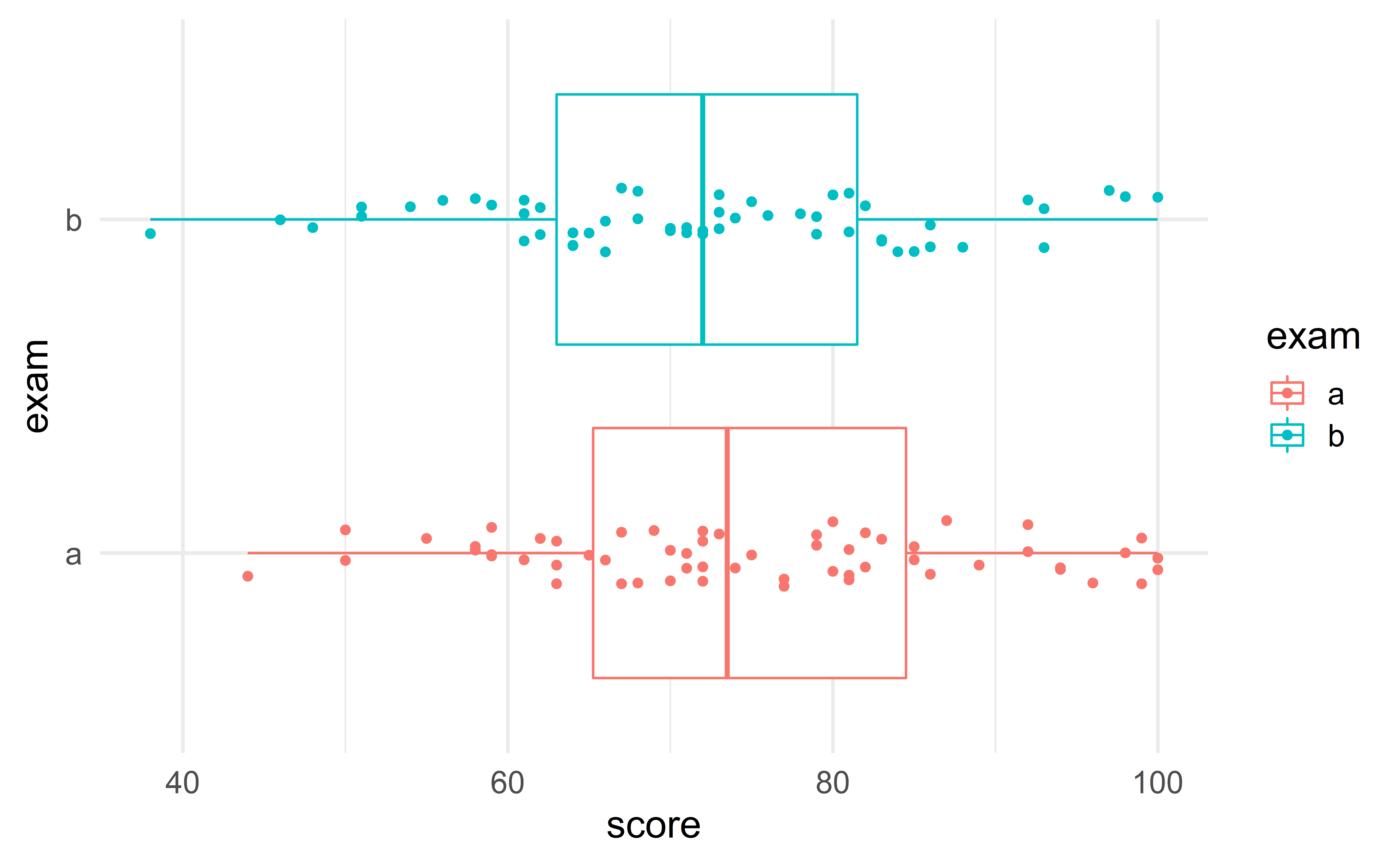
Group exercise - two proportions

Compute are \(\bar{x}_a\), \(\bar{x}_b\) and \(\bar{x}_{diff}\)? Do you intuitively feel that the data provide convincing evidence that the two exams are not equally difficult?

Hint: use the command summarize.

d <- openintro::classdata %>% 
  filter(lecture %in% c("a", "b")) %>%
  rename(score = m1, exam = lecture)
03:00

Hypothesis test via simulation

\(H_0:\mu_{diff}=0\)

\(H_a:\mu_{diff}\neq 0\)

  • Simulate many samples under \(H_0\) (no difference)

  • Determine if the observed data could have plausibly arisen under \(H_0\)

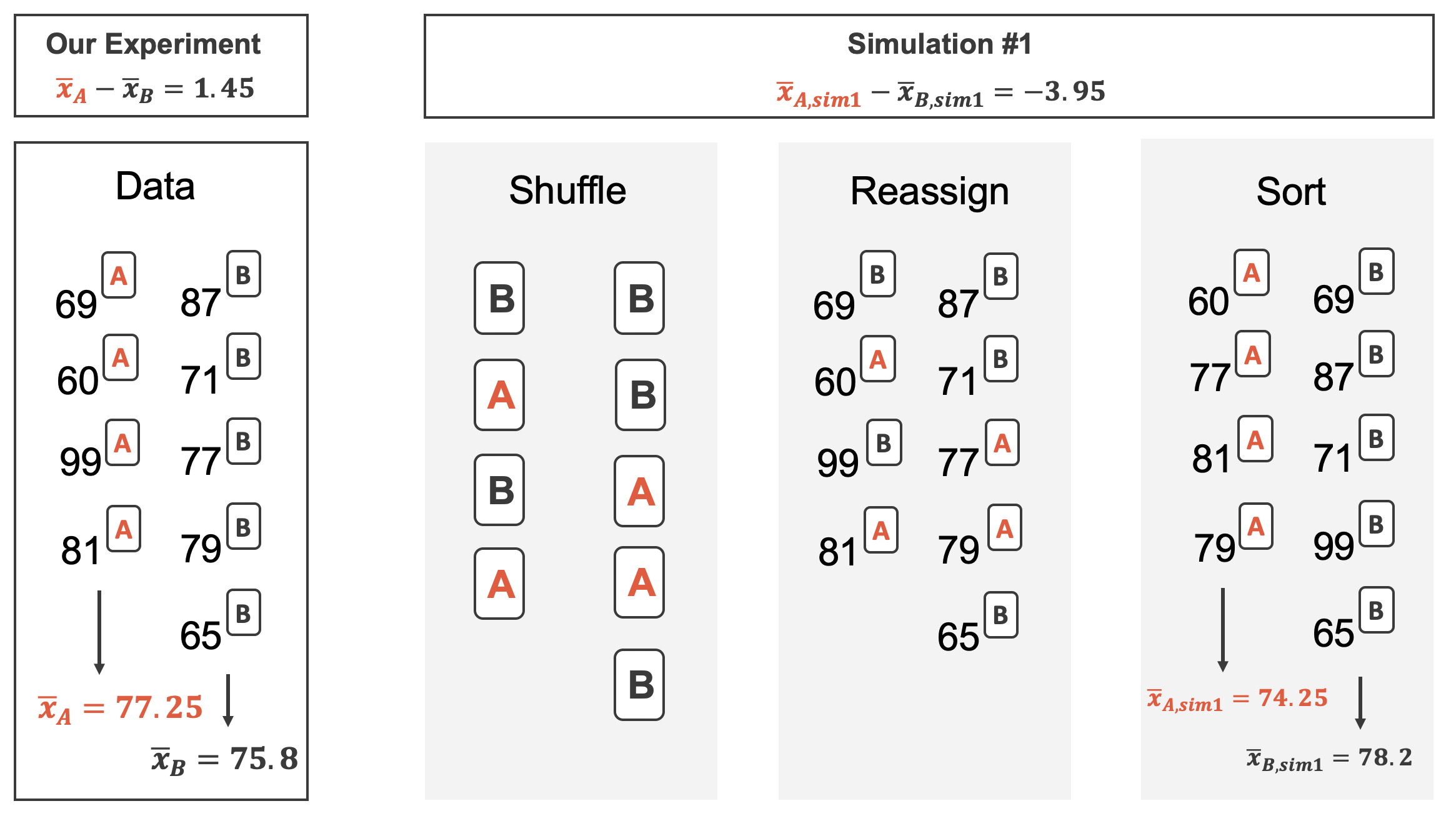
Simulating under \(H_0\)

Under \(H_0\), there is no difference between the two exams

\(\Rightarrow\) the score is independent of the type of exam

\(\Rightarrow\) randomly re-assign the scores independently of the exam type.

Tip

This is very similar to the procedure for two proportions.

Source: IMS

d_sim <- d %>% mutate(score = sample(score)) # shuffle the scores
d_sim
# A tibble: 113 x 2
   score exam 
   <dbl> <fct>
 1    67 a    
 2    93 a    
 3    82 a    
 4    82 a    
 5    70 a    
 6    82 a    
 7    66 a    
 8    84 a    
 9    50 a    
10    64 a    
# ... with 103 more rows

Function for computing the test statistic

compute_x_diff <- function(data){
  x_bar <- data %>%
    group_by(exam) %>%
    summarize(x_bar = mean(score))
  x_diff_bar <- x_bar$x_bar[1] - x_bar$x_bar[2]
  return(x_diff_bar)
}
compute_x_diff(d_sim)
[1] -0.437931

For-loop for simulating under \(H_0\)

# Setup
results   <- tibble(x_diff_bar = numeric())

# Simulations
set.seed(0)
for(i in 1 : 1e3){
  d_sim <- d %>% mutate(score = sample(score)) # simulate under H0
  x_diff_bar <- compute_x_diff(d_sim) # test statistic
  results <- results %>% add_row(x_diff_bar)
}

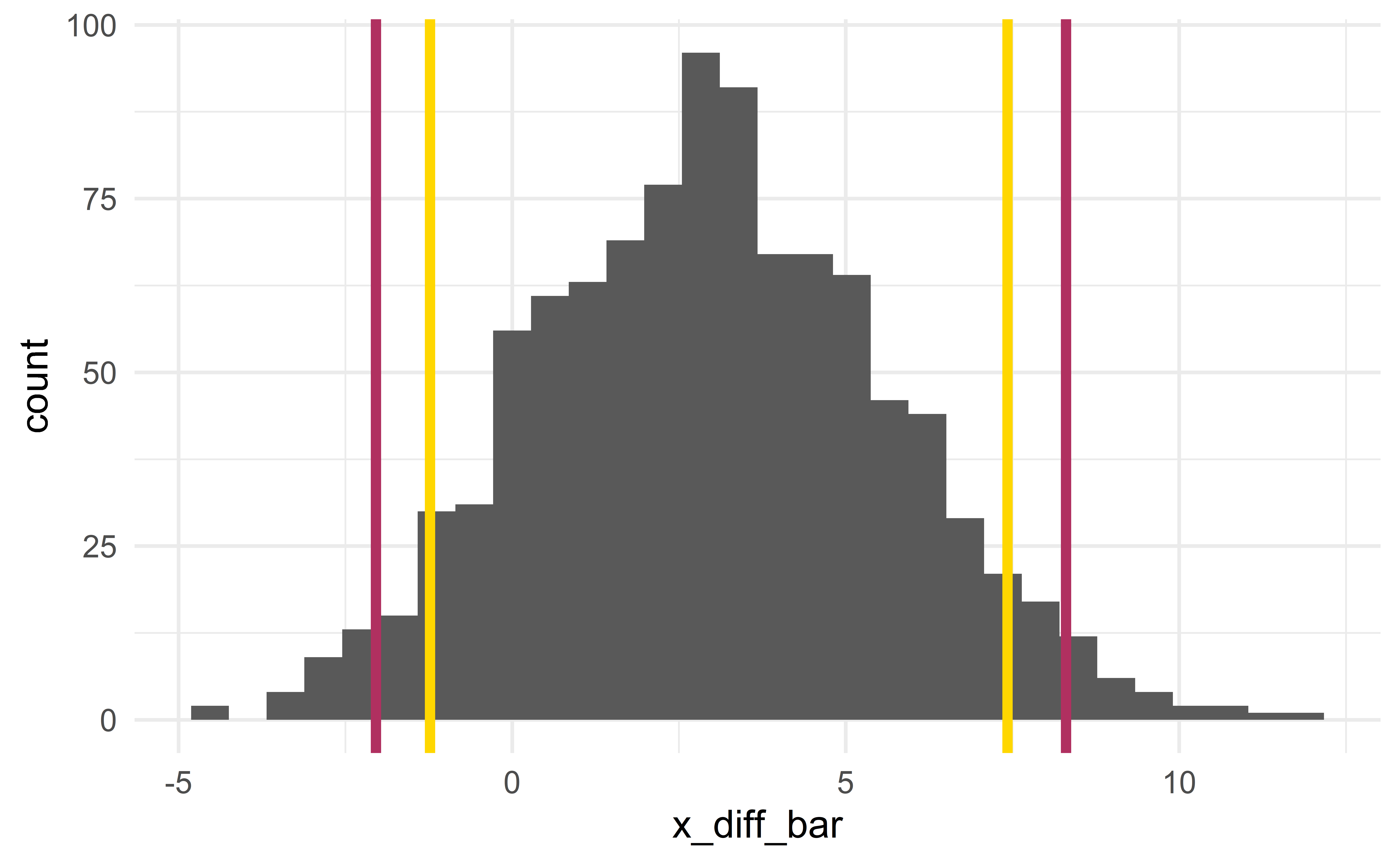
Sampling distribution

x_diff_obs <- compute_x_diff(d)
x_diff_obs
[1] 3.139812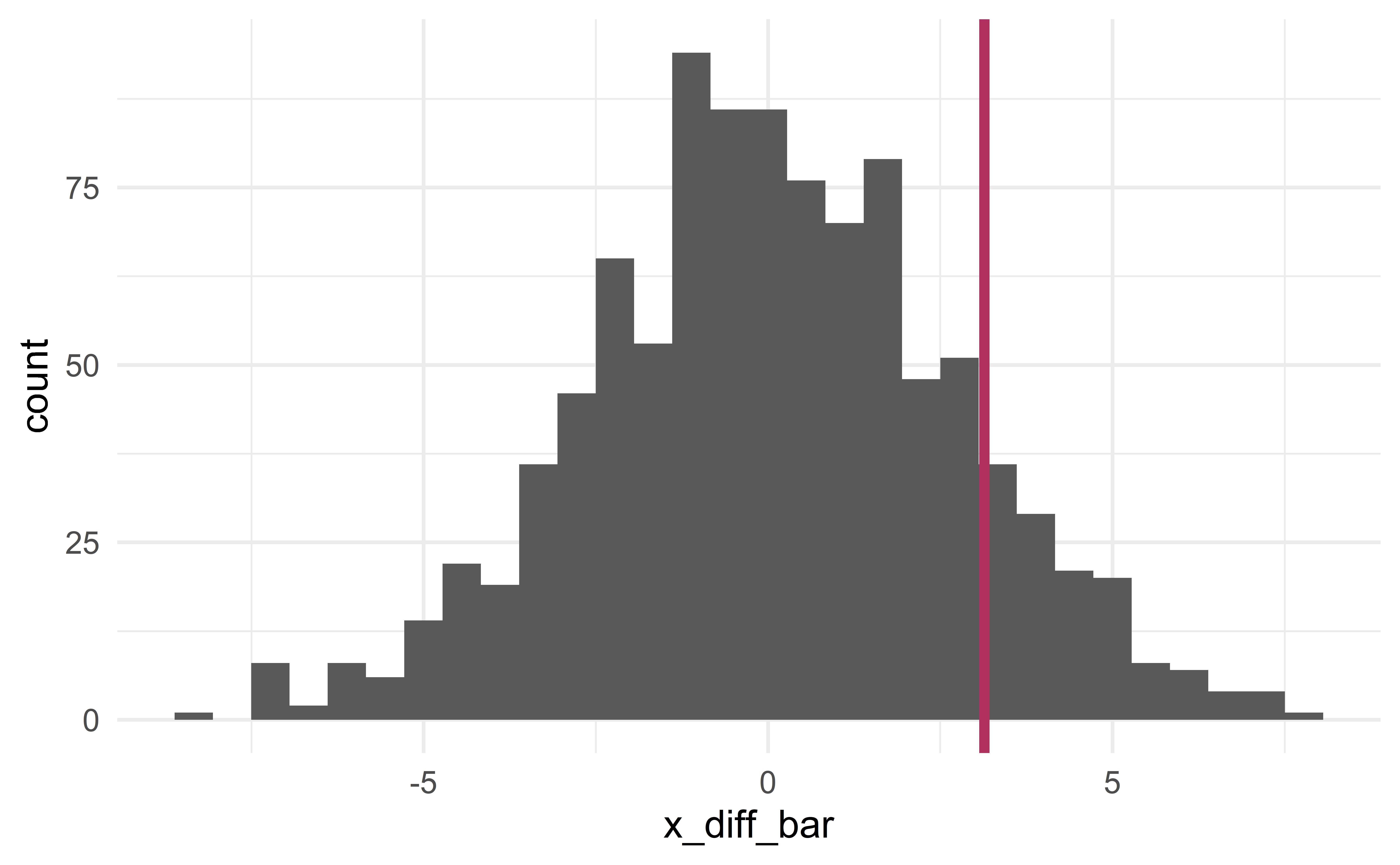
ggplot(results) + 
  geom_histogram(aes(x_diff_bar)) +
  geom_vline(xintercept = x_diff_obs, col = "maroon", size = 2)

p-value

  • the probability that \(\bar{x}_{diff}^{sim}\ge\) 3.1 or \(\bar{x}_{diff}^{sim}\le\) -3.1.
results %>%
  mutate(is_more_extreme = x_diff_bar >= x_diff_obs | x_diff_bar <= -x_diff_obs) %>%
  summarize(p_value = mean(is_more_extreme))
# A tibble: 1 x 1
  p_value
    <dbl>
1   0.227

Conclusion

Using the usual significance level \(\alpha = 0.05\), we fail to reject the null hypothesis

  • it is plausible that the observed difference in scores is due to random luck
  • the difference is not statistically significant.

Group exercise - HT

Exercises 20.3 and 20.7

03:00

Confidence interval via bootstrap

Bootstrap CI

Same idea as before: sample with repetition from the observed data to construct many bootstrap samples.

Bootstrap samples \(\Rightarrow\) sampling distribution \(\Rightarrow\) CI

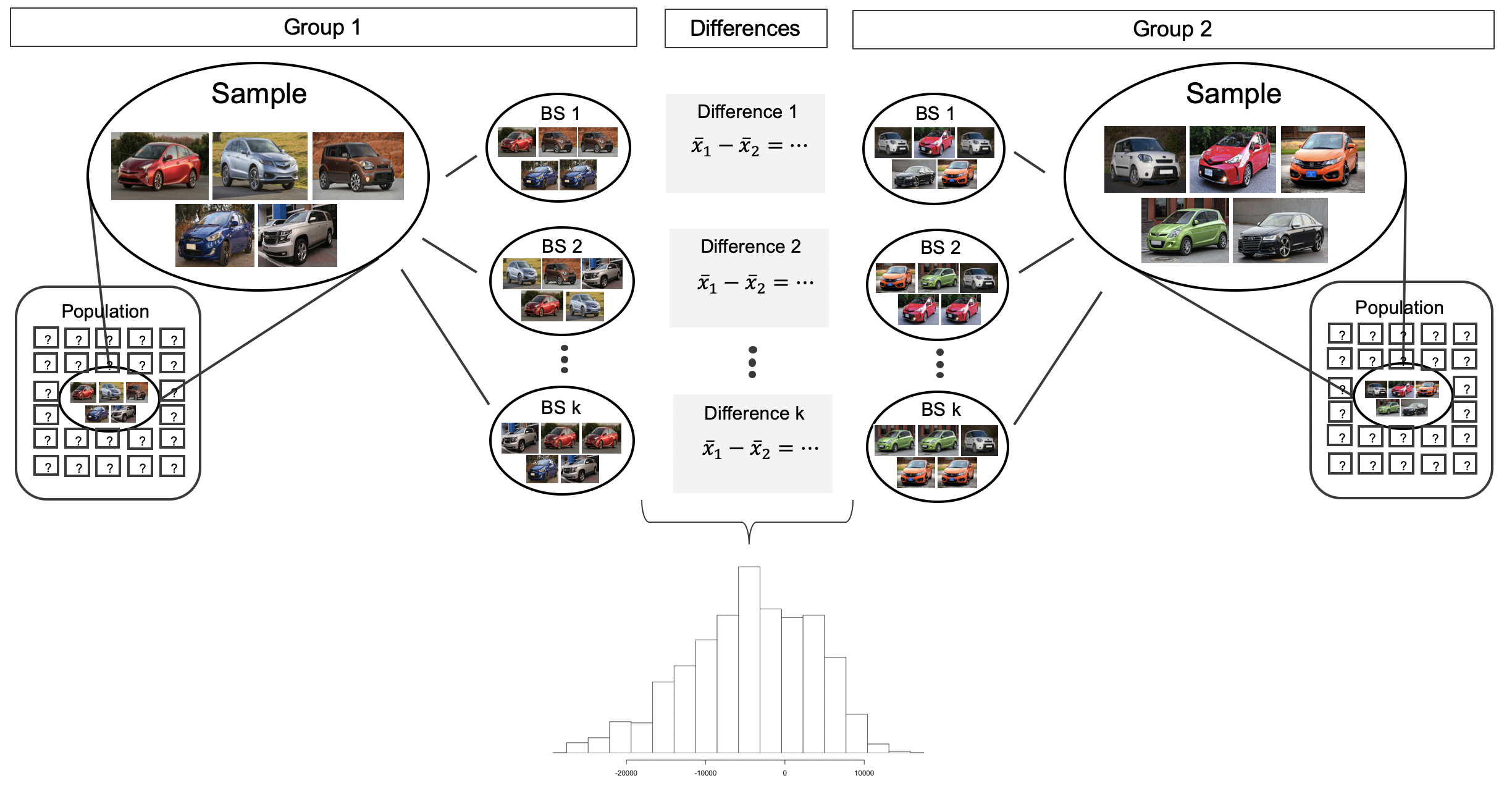
Source: IMS

Bootstrap in R

sample_observed_a <- d %>% filter(exam == "a")
sample_observed_b <- d %>% filter(exam == "b")

set.seed(0)
sample_bootstrap(sample_observed_a) # bootstrap sample
# A tibble: 58 x 2
   score exam 
   <dbl> <fct>
 1    58 a    
 2    59 a    
 3    81 a    
 4    71 a    
 5    67 a    
 6    58 a    
 7    80 a    
 8    72 a    
 9    58 a    
10    72 a    
# ... with 48 more rows
sample_bootstrap(sample_observed_b) # bootstrap sample
# A tibble: 55 x 2
   score exam 
   <dbl> <fct>
 1    61 b    
 2    83 b    
 3    68 b    
 4    71 b    
 5    82 b    
 6    46 b    
 7    78 b    
 8    72 b    
 9    64 b    
10    83 b    
# ... with 45 more rows

results <- tibble(x_diff_bar = numeric())
for(i in 1 : 1e3){
  d_boot_a   <- sample_bootstrap(sample_observed_a) # bootstrap sample
  d_boot_b   <- sample_bootstrap(sample_observed_b) # bootstrap sample
  x_diff_bar <- compute_x_diff(rbind(d_boot_a, d_boot_b)) # bootstrap statistic
  results    <- results %>% add_row(x_diff_bar)
}
quantile(results$x_diff_bar, c(0.05 , 0.95 )) %>% signif(2) # 90% CI
  5%  95% 
-1.2  7.4 
quantile(results$x_diff_bar, c(0.025, 0.975)) %>% signif(2) # 95% CI
 2.5% 97.5% 
 -2.0   8.3 

ggplot(results) +
  geom_histogram(aes(x_diff_bar))  + 
  geom_vline(xintercept = quantile(results$x_diff_bar, c(0.05 , 0.95 )), col = "gold1", size = 2) + # 90% CI 
  geom_vline(xintercept = quantile(results$x_diff_bar, c(0.025, 0.975)), col = "maroon", size = 2) # 95% CI

CI and HT

Two sides of the same coin

The two CIs include 0. This indicates that 0 is a plausible value for the difference in mean in the population. This is exactly what the HT concluded!

Individual exercises - CI

Exercise 20.5 part a only

03:00

Paired means

Paired data

Paired data: two groups in which each observation in one group has exactly one corresponding observation in the other group.

Example: pre/post-evaluations; supermarket items; batteries and electronic devices; tires and cars.

Paired data are like one mean data

Paired data can be analyzed like the one-mean case (case 3)!

Example – tire brand

We want to compare the longevity of two brands of tire. The response variable is tire tread after 1000 miles.

25 cars drove 1000 miles. On each car, one tire was from Smooth Turn and another one was from Quick Spin. The other two tires were baseline tires.

set.seed(1)
bias <- runif(25, -0.01, 0.01)
brandA <- rnorm(25, bias + 0.310, 0.003)
brandB <- rnorm(25, bias + 0.308, 0.003)
car <- c(paste("car", 1:25))
miny <- min(brandA, brandB) - .003
maxy <- max(brandA, brandB) + .003
tires <- tibble(
  tread = c(brandA, brandB),
  car = rep(car, 2),
  brand = c(rep("Smooth Turn", 25), rep("Quick Spin", 25))
) %>%
  arrange(car)
head(tires)
# A tibble: 6 x 3
  tread car    brand      
  <dbl> <chr>  <chr>      
1 0.304 car 1  Smooth Turn
2 0.307 car 1  Quick Spin 
3 0.302 car 10 Smooth Turn
4 0.303 car 10 Quick Spin 
5 0.307 car 11 Smooth Turn
6 0.305 car 11 Quick Spin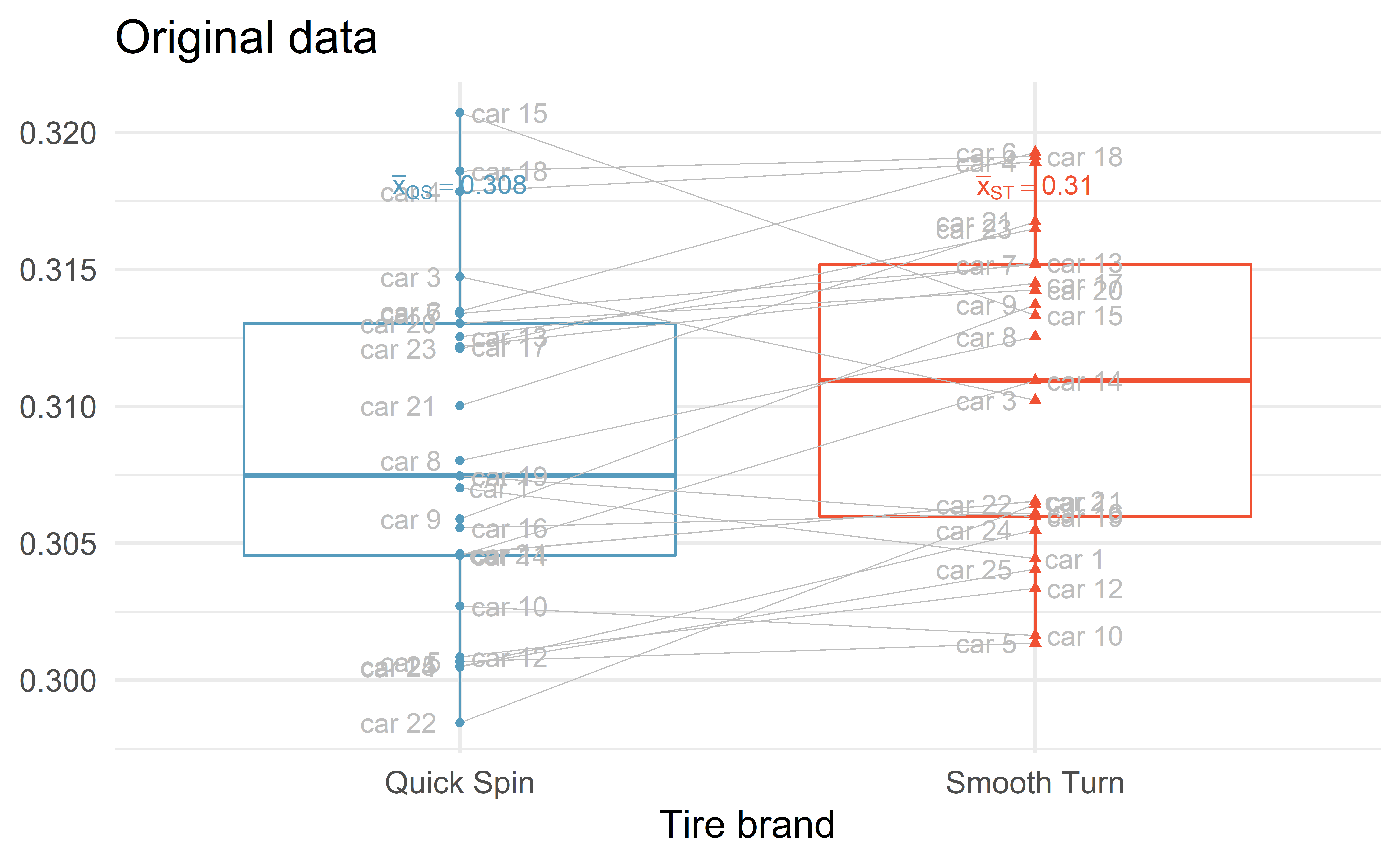

Source: IMS

Individual exercise - paired data

Do you intuitively feel that the tire data provide convincing evidence that one tire is more durable than the other?

Exercises 21.1, 21.3 and 21.5

04:00

CI via booststrap

Exactly the same as with one mean (case 3).

tires_diff <- tires %>% 
  pivot_wider(names_from = brand, values_from = tread) %>%
  mutate(tread_diff = `Smooth Turn` - `Quick Spin`) %>%
  select(car, tread_diff)
head(tires_diff)
# A tibble: 6 x 2
  car    tread_diff
  <chr>       <dbl>
1 car 1    -0.00258
2 car 10   -0.00107
3 car 11    0.00192
4 car 12    0.00251
5 car 13    0.00271
6 car 14    0.00639

Simply construct a CI for the variable tread_diff with bootstrap samples.

Group exercise - CI for paired data

Use the R code from the one-mean case (case 3) to construct a CI for the difference in tire tread.

10:00

HT via simulation

\(H_0:\mu_{diff}=0\)

\(H_a:\mu_{diff}\neq 0\)

  • Simulate many samples under \(H_0\) (no difference)

  • Determine if the observed data could have plausibly arisen under \(H_0\)

Simulating under \(H_0\)

Under \(H_0\), there is no difference between the two tire brands

\(\Rightarrow\) tire tread is independent of tire brand

\(\Rightarrow\) randomly re-assign tire tread independently of tire brand.

Re-assign within

The re-assignment happens within a car; either switch the two values or keep the original allocation.

Re-assigning two cars

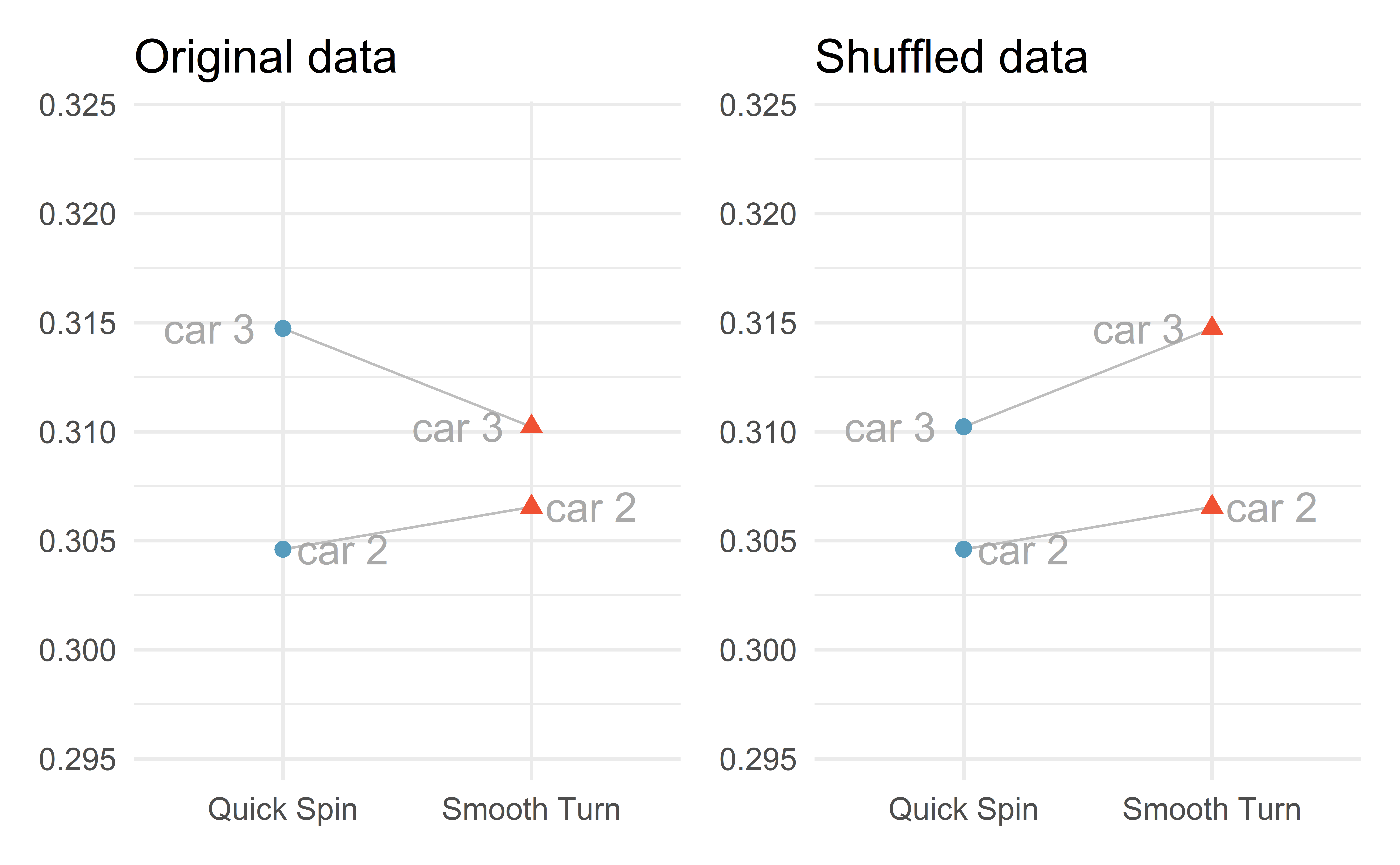
Re-assigning all cars

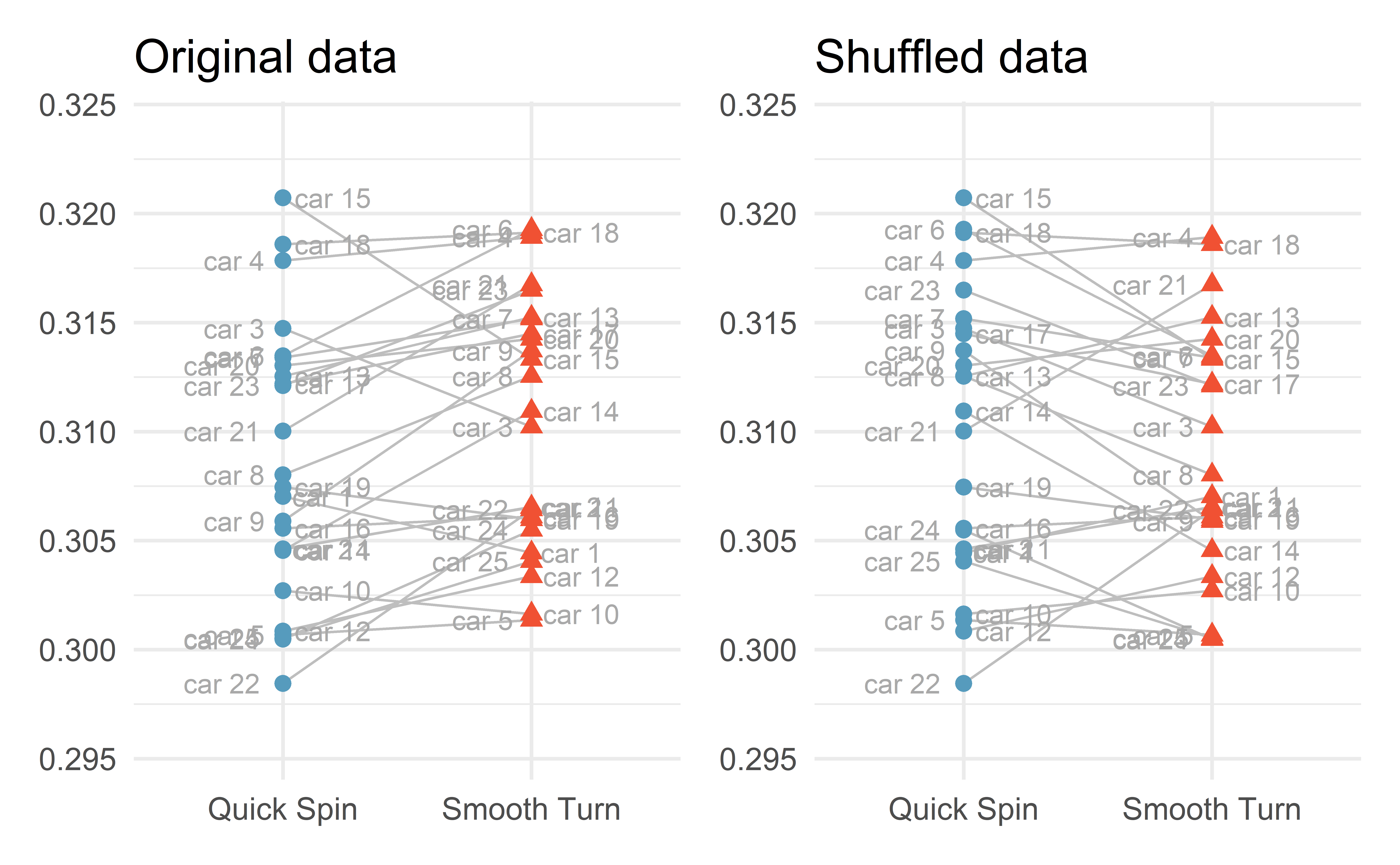
Individual exercise - simulated difference

Exercise 21.9

02:00

R function to shuffle data

shuffle_data <- function(data){
  tires %>%
  group_by(car) %>%
  mutate(tread = sample(tread))
}

set.seed(0)
tires_shuffled <- shuffle_data(tires)
head(tires)
# A tibble: 6 x 3
  tread car    brand      
  <dbl> <chr>  <chr>      
1 0.304 car 1  Smooth Turn
2 0.307 car 1  Quick Spin 
3 0.302 car 10 Smooth Turn
4 0.303 car 10 Quick Spin 
5 0.307 car 11 Smooth Turn
6 0.305 car 11 Quick Spin 
head(tires_shuffled)
# A tibble: 6 x 3
# Groups:   car [3]
  tread car    brand      
  <dbl> <chr>  <chr>      
1 0.307 car 1  Smooth Turn
2 0.304 car 1  Quick Spin 
3 0.303 car 10 Smooth Turn
4 0.302 car 10 Quick Spin 
5 0.307 car 11 Smooth Turn
6 0.305 car 11 Quick Spin

R function for computing the test statistic

compute_stat <- function(data){
  
  data %>% 
    pivot_wider(names_from = brand, values_from = tread) %>%
    mutate(tread_diff = `Smooth Turn` - `Quick Spin`) %>%
    ungroup() %>%
    summarise(x_diff_bar = mean(tread_diff)) %>%
    pull(x_diff_bar)
  
}
compute_stat(tires_shuffled)
[1] -0.001036578

For-loop for simulating under \(H_0\)

# Setup
results   <- tibble(stat_sim = numeric())

# Simulations
set.seed(0)
for(i in 1 : 1e3){
  d_sim    <- shuffle_data(tires) # simulate under H0
  stat_sim <- compute_stat(d_sim) # test statistic
  results  <- results %>% add_row(stat_sim)
}

Sampling distribution

stat_obs <- compute_stat(tires)
stat_obs
[1] 0.0020934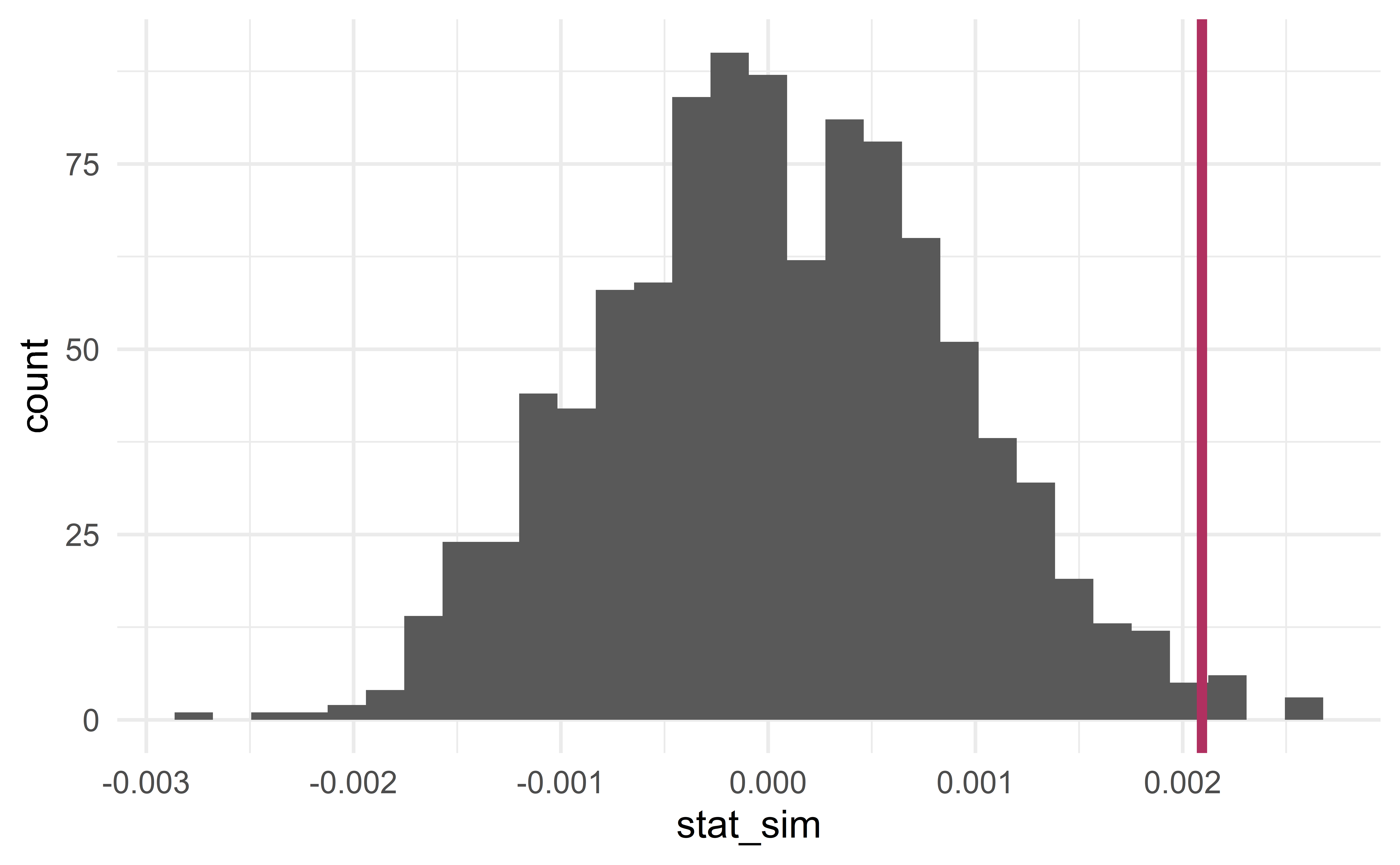
ggplot(results) + 
  geom_histogram(aes(stat_sim)) +
  geom_vline(xintercept = stat_obs, col = "maroon", size = 2)

p-value and conclusion

  • the probability that \(\bar{x}_{diff}^{sim}\ge\) 0.0021 or \(\bar{x}_{diff}^{sim}\le\) -0.0021.
results %>%
  mutate(is_more_extreme = stat_sim >= stat_obs | stat_sim <= -stat_obs) %>%
  summarize(p_value = mean(is_more_extreme))
# A tibble: 1 x 1
  p_value
    <dbl>
1   0.012

Using the usual significance level \(\alpha = 0.05\), we reject \(H_0\).

Individual exercise - HT

Exercise 21.11

02:00

To pair or not to pair?

Always pair

If the data can paired, you should always do it! Pairing data yields an analysis that is more powerful:

  • narrower CI

  • smaller p-values

HT for two means (case 4)

Let us conduct a hypothesis test for the tire data, but this time without pairing the data.

\(\Rightarrow\) This is simply a hypothesis test for two means.

Larger p-value

compute_x_diff <- function(data){
  x_bar <- data %>%
    group_by(brand) %>%
    summarize(x_bar = mean(tread))
  x_diff_bar <- x_bar$x_bar[1] - x_bar$x_bar[2]
  return(x_diff_bar)
}
compute_x_diff(tires)
[1] -0.0020934
results   <- tibble(x_diff_bar = numeric())
set.seed(0)
for(i in 1 : 1e3){
  d_sim      <- tires %>% mutate(tread = sample(tread)) # simulate under H0
  x_diff_bar <- compute_x_diff(d_sim) # test statistic
  results    <- results %>% add_row(x_diff_bar)
}
x_diff_obs <- compute_x_diff(tires)
results %>%
  mutate(is_more_extreme = abs(x_diff_bar) >= abs(x_diff_obs)) %>%
  summarize(p_value = mean(is_more_extreme))
# A tibble: 1 x 1
  p_value
    <dbl>
1   0.229

The p-value is larger than \(\alpha=0.05\); we fail to reject the null hypothesis.

ggplot(results) + 
  geom_histogram(aes(x_diff_bar)) +
  geom_vline(xintercept = x_diff_obs, col = "maroon", size = 2)

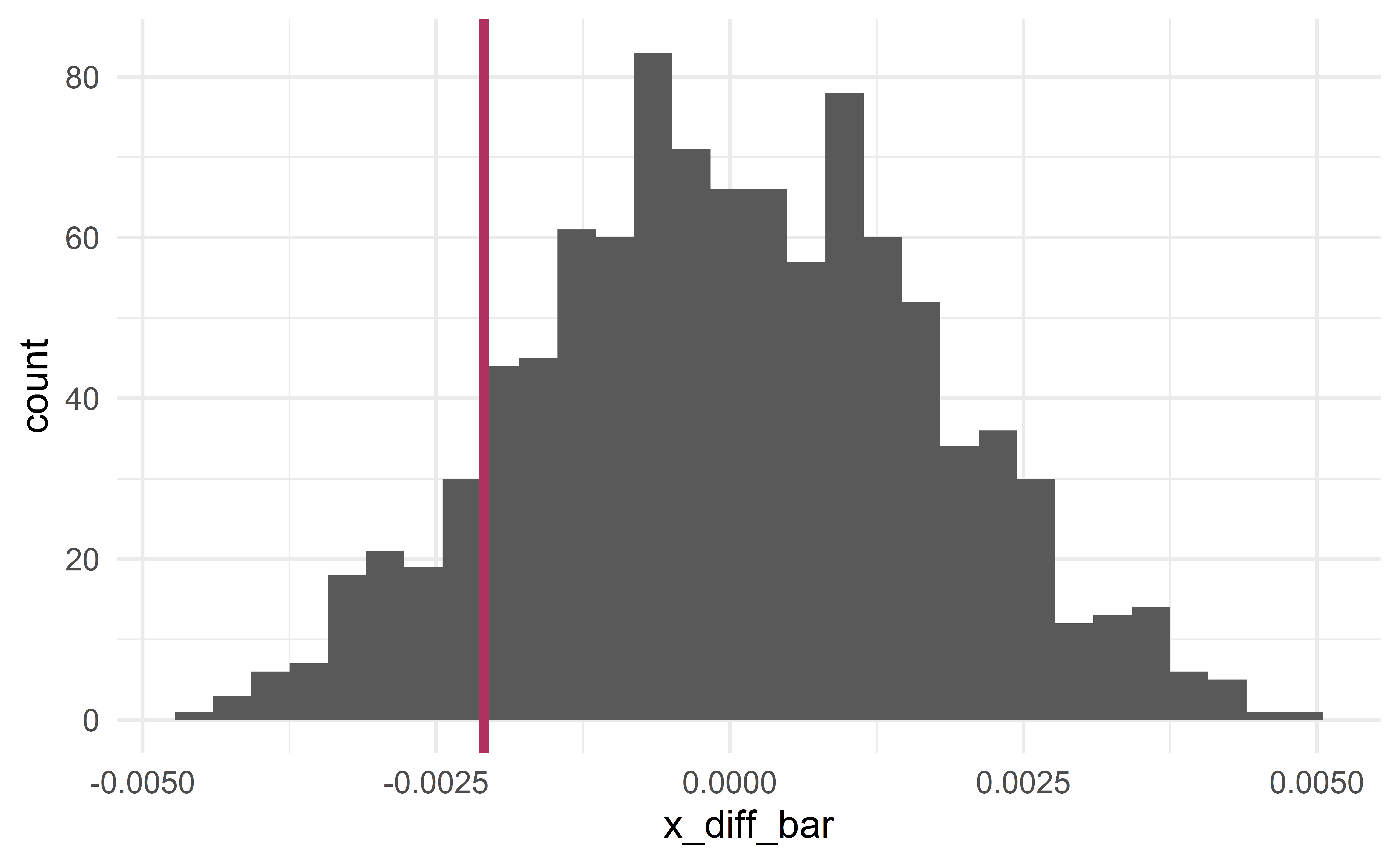
Group exercise - wider CI

Use the R code from the two-mean case (case 4) to construct a CI for the difference in tire tread (the observations are not paired).

You should obtain a wider interval.

10:00

Recap

Recap

  • The normal distribution
  • One mean (case 3)
  • Two means (case 4)
  • Paired means (case 3)

https://rmorsomme.github.io/website/